CHANCE News 11.04
|
| Powerlifting | ||
| number of official tests | 185 | |
| number of elite competitors: | 50 | |
| chance of being tested: | 370% | |
| Athletics | ||
| tests: | 605 | |
| elite competitors | 250 | |
| chance of being tested | 242% |
etc.
The Guardian, 27 April 2002
David Fisman suggested the Forsooth item:
It's a fact. Interest rates are at their lowest point this year. But the likelihood of them going up in the near future is a very real possibility [sic].
Ditech.com CNN commercial
An interesting website: Plus Magazine. From this site we read:
Plus is part of the Millennium Mathematics Project, a long term national initiative based in Cambridge and active across the UK and internationally. The MMP aims to help people of all ages and abilities share in the excitement of mathematics and understand the enormous range and importance of its applications to science and commerce. It works to change people's attitudes to maths, to act as a national focus for renewing and improving appreciation of the dynamic importance of maths and its applications, and to demonstrate the vital contribution of maths to shaping the everyday world.
Plus has had a number
of articles related to probability and statistics including:
What
a coincidence! , by Geoffrey Grimmett. The current issue has an article
"Beyond
reasonable doubt" described as follows:
In 1999 solicitor Sally Clark was found guilty of murdering her two baby sons. Highly flawed statistical arguments may have been crucial in securing her conviction. As her second appeal approaches, Plus looks at the case and finds out how courts deal with statistics.
This is an issue that has been in the U.K. news a great deal and we should have written about it earlier. We hope this article makes up for our neglect.
Coincidences have been in the news recently. The New York Times Magazine had the following feature article:
The
odds of that.
New York Times, 11 August, 2002, section 6; page 31; Magazine Desk
Lisa Belkin
In this article on coincidences the author illustrates many of the issues involved with coincidences with a conspiracy story that appeared on the web and in the news. A good account of this story is found in " Scientists' deaths are under the microsc ope" written by Alanna Mitchell, Simon Cooper and Carolyn Abraham that appeared in the May 4, 2002 issue of the Globe and Mail newspaper. In this article we read:
It's a tale only the best conspiracy theorist could dream up.
Eleven microbiologists mysteriously dead over the span of just five months. Some of them world leaders in developing weapons-grade biological plagues. Others the best in figuring out how to stop millions from dying because of biological weapons. Still others, experts in the theory of bioterrorism.
Throw in a few Russian defectors, a few nervy U.S. biotech companies, a deranged assassin or two, a bit of Elvis, a couple of Satanists, a subtle hint of espionage, a big whack of imagination, and the plot is complete, if a bit reminiscent of James Bond.
Of course the fact that these deaths occurred around the time of the anthrax scare enhanced the conspiracy theory. In her article, Lisa Belkin shows that, on a closer look, one finds that not all of the researchers were microbiologists and not all the deaths were as mysterious as they first appeared. She does a good job of showing that this cluster, like most clusters turns out not to be so surprising when we look at the big picture. While it is a long and well written article about why coincidences in general seldom seldom turn out to be so surpising when looked with the proper perspective, we think our readers would be most interested in the many quotes of the experts. Here are a few of these:
Believing in fate, or even conspiracy, can sometimes be more comforting than facing the fact that sometimes things just happen.
John A. Paulos.
The
really unusual day would be one where nothing unusual happens. Given that
there are 280 million people in the United States, 280 times a day, a one-in-a-million
shot is going to occur.
We can never say for a fact that something isn't a conspiracy. We can just
point out the odds that it isn't.
Bradley Efron
Imagine a meadow and then imagine placing your finger on a blade of grass. The chance of choosing exactly that blade of grass would be one in a million or even higher, but because it is a certainly that you will choose a blade of grass, the odds of one particular one being chosen are no more or less than the one to either side.
Bradley Efron
We are hard-wired to overreact to coincidences. It goes back to primitive man. You look in the bush, it looks like stripes, you'd better get out of there before you determine the odds that you're looking at a tiger. The cost of being flattened by the tiger is high. Right now, people are noticing any kind of odd behavior and being nervous about it.
Persi Diaconis
Belkin describes an interesting experiment carried out by Ruma Falk:
She (Ruma Falk) visited several large university classes, with a total of 200 students, and asked each student to write his or her birth date on a card. She then quietly sorted the cards and found the handful of birthdays that students had in common. Falk wrote these dates on the blackboard. April 10, for instance, Nov. 8, Dec. 16. She then handed out a second card and asked all the students to use a scale to rate how surprised they were by these coincidences.
The cards were numbered, so Falk could determine which answers came from respondents who found their own birth date written on the board. Those in that subgroup were consistently more surprised by the coincidence than the rest of the students. "It shows the stupid power of personal involvement," Falk says.
The first sentence is a little confusing but it is clear what the experiment was.
Belkin also describes a new book "When God Winks: How the Power of Coincidence Guides Your Life" written by Squire Rushnell, former executive at ABC Television Network. She remarks that this book was published by a small press shortly before before Sept. 11 and sold well without much publicity and it will be released with great fanfare by Simon & Shuster in October. We found the book in our local bookstore and the cover greeted us by saying: It is not an accident that you just picked up When God Winks.
While we try to persuade our students that most coincidences are really not surprising at all, Rushnell wants to convince his readers that not only are they surprising, but they were sent by God as "winks" to guide their lives. After describing how his life and successes were guided by coincidences, readers are encourage to keep a "wink diary" in which they write down coincidences in their lives that have had significant effects on their lives, such as coincidences that led them to the person they married, a new job, a new outlook on life, etc.
Having read the book we think Rushnell has an easier sell then we do.
There have of course been many articles on coincidences. Two of our favorites are:
(1) Methods for studying coincidences. Journal of American Statistical Association, Persi Diaconis and Fredrick Mosteller, Vol. 84, Issue 408, pp. 853-861. Available from jstor.
(2) Coincidences: Remarkable or Random? Skeptical Inquirer, September-October 1998.
It is hard to write an article on coincidences and not mention the Lincoln-Kennedy story and the NYTimes article is no exception. Belkin writes:
It is always possible to comb random data to find some regularities. A well-known qualitative example is the comparison of coincidences in the lives of Abraham Lincoln and John Kennedy, two presidents with seven letters in their last names, and elected to office 100 years apart, 1860 and 1960.
Both were assassinated on Friday in the presence of their wives, Lincoln in Ford's theater and Kennedy in an automobile made by the Ford motor company.
Both assassins went by three names: John Wilkes Booth and Lee Harvey Oswald, with fifteen letters in each complete name.
Oswald shot Kennedy from a warehouse and fled to a theater, and Booth shot Lincoln in a theater and fled to a barn (a kind of warehouse).
Both succeeding vice-presidents were southern Democrats and former senators named Johnson (Andrew and Lyndon), with thirteen letters in their names and born 100 years apart, 1808 and 1908.
The Skeptical Inquirer article discusses its "Spooky presidential coincidences contest." This contest asked readers to send in similar coincidences between other pairs of presidents. The contest itself is described in the Spring 1992 issue of Skeptical Inquirer and the winners in the Winter 1993 issue. Co-winner Chris Fishel managed to come up with a list of coincidences between 21 different pairs of presidents none of which involved fewer than 6 coincidences. Fishel wrote:
After discovering that the lists of coincidences can be devised for pairings as unlikely as Teddy Roosevelt and Millard Fillmore, I think a really challenging contest would be finding a pair of presidents with fewer than five coincidences between them.
Our own feeling is that the best coincidences to use in class are those like the Bible Code controversy where you can actually compute some probabilities and replicate experiments. For some recent replications of Bible Codes experiments see the Gans report.
DISCUSSION QUESTIONS:
(1) The winning numbers for the New York Numbers Lottery on September 11 2002 were 9-1-1. If you are called by your local newspapers to comment on this apparent coincidence what would you tell them?
(2) According to Newsday (September 13) lottery officials reported that in the last 5000 plays of their numbers lottery, 9-1-1 has been the winning numbers 5 times. Is this too good to be true?
Erika Rasmusson, a freelance writer writing a story on coincidences for Redbook magazine, asked us the following question:
What are the odds that there is more than one child named Emily in your kid's kindergarten class this year, assuming a class size of 20 and an even split boys and girls (26,132 Emilys born in 1997--most popular girl's name that year, according to the Social Security Administration)?
Also, what are the odds that there is more than one child in the class named Michael? (There were 38,406 Michaels born in 1997--most popular boy's name that year.)
We found this an interesting estimation problem. As we remarked in Chance News 8.06, Michael Shackleford maintains the well-known odds web site The Wizard of Odds. While working for the Social Security Administration, Michael started posting on the Social Security web site each year the list of most popular babies' names. Michael wrote us that coincidentally:
My daughter is in kindergarten and has 25 in her class. She was born in '97 and was the one who started this whole study, because, as a Michael, I didn't want to give her a top-40 name.
At the Social Security web site we find a list of the 1000 most popular girl's and boy's names for babies born in 1997 along with how many babies had each of these names. This is based on information obtained when a social security number is requested. No attempt is made to equate similar names so, for example, Ann and Anne are considered different names.
As Erika said, in 1997 Emily was the winner for girls with 26,132 Emilys and Michael the winner for boys with 38,406 Michaels. There are a total of 1,447,377 girls who have one of the 1000 most popular girl's names and a total of 1,748,339 boys who have one of the 1000 most popular boy's names. This accounts for 3,195,716 of the babies born in 1997.
From the 1997 CDC National Vital Statistics Report we find that an estimated 3,880,894 babies were born in 1997. If we assume the usual 1.05 sex ratio, then we would estimate 1,893,310 girls and 1,987,770 boys born in 1997. Of course, these are greater than the the top 1000 totals because there are children whose names did not make the top 1000 and also who did not get social security numbers. The latter number is probably small. The request for a social security number can be made at the hospital when the birth certificate information is given and this number is needed to obtain a tax deduction for a child. Thus one can believe that most babies are assigned a social security number at birth.
We now want to estimate the probability p that a randomly chosen 1997 baby is named Emily. We can view the Social Security data as as a sample from the population of 1997 births. Then, our estimate for p is 26,132/n where n is the number of 1997 babies with social security numbers. We do not know n but we know that it is at least 1,447,377 and at most 1,893,410. Using these two values for n gives us lower and upper bounds for p of .0131 and 0181.
We can use these probabilities to obtain an upper and lower bound for the probability of finding 2 or more girls named Emily in your Kindergarten class. This is a simple binomial distribution problem. Carrying out the relevent calculations, using our lower and upper bounds for p, we find that the probability that there are 2 or more Emilys in a class with 10 boys and 10 girls is between .007 and .013. Thus we might estimate the probability to be about 1%.
Similar computations show that the probability of 2 or more Michaels in your Kindergarten class is between .0152 and .0193, so we might estimate about a 1.7% chance of having 2 or more Michaels in your class.
Of course, these are not small enough to be surprising and too small to be expected so this turns out to not be a very interesting coincidence problem. We bet that this example will not end up in Erika's article! However, if she had asked the same questions for two or more boys name Laurie or two or more girls named Jeanne in a Kindergarten class, you would be asking: What is the probability of that?
DISCUSSION QUESTIONS:
(1) The names Laurie and Jeanne do not make the list of the first 1000 popular names. Now how do we answer the question: What is the probability of two girls named Jeanne in your kindergarten class?
(2) Do you think the
sample of babies born in 1997 who have social security numbers can be considered
a random sample of the set of all babies born in 1997? Does this matter
for our problem?
John Paulos and Jordan Ellenberg have Internet columns of interest to Chance readers.
John writes a monthly column "Who's counting?" for ABCNews.com.
His current
column "The 9-11 Lottery coincidence: analysis shows such coincidences
aren't so unusual" does just what the title suggests. Readers might
also enjoy John's previous column "Weighing risks: relative risks,
hormone treatments and difficult decisions" available at the
archives
of his columns.
Jordan writes an occasional column "Do the math. A mathematician's guide to the news" for Slate magazine. His current column is "Don't worry about grade inflation." Jordan argues that even if you had only two grades, A and A-, statistical theory assures that you will be able to differentiate students of different abilities using their overall history of grades. Of course, Jordan's statistical argument is even more convincing with more grades. Readers provide interesting comments on Jordon's ideas.
Readers might also enjoy Jordan's previous column "Blinded by science:
explaining the media's obsession with Stephen Wolfram's A New Kind
of Science. You can find this article by searching for "Ellenberg"
on the Slate homepage.
Statisticians count euros and find more than money.
The New York Times, 2 July, 2002, F3
Otto Pohl
On January 1, 2002, euro coins began spreading across Europe. Twelve countries mint their own distinctive coin, but all euros are legal tender in any of the European Union's member nations. This article describes the efforts of two groups of mathematicians to study the diffusion and distribution of the coins throughout Europe.
One group, led by Dr. Dietrich Stoyan, professor of statistics at the University of Freiberg in Germany, is using a differential equations based diffusion model, while the second group, based at the University of Amsterdam and supported by the science magazine "Natuur & Techniek" and the study group Mathematics with Industry, is using Markov Chains to study the distribution of the coins. Each country produces a fixed proportion of euros that is determined by that country's percentage of the overall European economy. (For example, Germany produces the largest percentage, 32.9%; France is next at 15.8%; Ireland and Finland, 2.1% each. A complete breakdown is available at the Freiberg site.)
According to the article, the Amsterdam group "assumes that a relatively constant percentage of Dutch coins will leave the Netherlands each month, and that a different, smaller, percentage of Dutch coins will return." (Presumably, similar figures are being used for the remaining euro-producing countries.) Each study relies, at least in part, on reports made to their website, where participants post "the contents of their wallets."
DISCUSSION QUESTIONS:
(1) Why do the Dutch researchers assume that a relatively constant percentage
of coins leave and return to Holland each month?
(2) Sampling.
(a) As mentioned in the article, each study relies on data provided by web site visitors. (The Dutch study actually enlists "EuroMeters" in advance, who record the coins in their possession once a month.) Comment on this method of taking a sample.
(b) As a school project, some students in math and statistics classes in Europe are periodically asked to bring in rolls of euros bought at a local bank. Comment on this method.
(c) What other sampling methods can you think of?
(3) The article states that "the Dutch group believes that half of all coins in Holland will be of foreign origin a year from now and that statistical equilibrium across Europe will be reached in five to seven years." How do you think they came up with these figures?
MIT
Vegas.
All things considered, National public radio 4, October 2002
Robert Siegal
Here is the abstract of this program:
Robert Siegal talks with Ben Mezrich about his new book called "Bringing Down the House." It's the story of six MIT students who won millions by counting cards in Vegas blackjack games. Eventually, the casinos caught on to their scheme and harassed them until they had to stop.
If you want to know more about how it was done read the article written by Mezrich for Wired News.
We received the following note from Michael Holaday:
The Grand Rapids (MI) Press for Monday, Aug 26,
2002, contained this snippet of Weather News by meteorologist Bill Steffen:
If you've planned an event for Saturday or Sunday this summer, odds are you've had sunshine and not even a passing shower. We've had 8.81 inches of rain since June 1st. Less than 7 percent of the rain has come on the weekends! Ninety-three percent of our summer rain has occurred between Monday and Friday.
If Steffen had cited the number of weekdays with rainfall I could have tested his data to see whether this pattern is particularly noteworthy. It strikes me that it may be unusual for 93 percent of the rainfall over a 13-week period to occur between Monday and Friday, but not especially remarkable since about 71 percent of the time occurs between Monday and Friday. If there is no "weekend effect," one could therefore assume that about 71 percent of the rainfall would occur on weekdays.
Michael wanted suggestions on how to test the significance of Steffen's observations. We decided to leave this to our readers or their students. The additional data that Michael wanted is available here. Please let us know if you or your students do come up with an answer for Michael.
In Chance News 7.07 we mentioned a study in Nature which purported to show that there was more rain on weekends on the Eastern coast suggesting that this could be the effect of pollution. You can listen to the author of the study on NPR here. On this program another weather expert is skeptical and suggests that their results could be due to chance. He said a longer range study would have to be done.
David Schultz at the National Severe Storms Laboratory, Norman, Oklahoma,
who himself wrote an article on this topic (1) told us that such a long
range study has been carried out by Mark P. DeLisi and others (2). Here
is their abstract:
Twenty years of precipitation data from seven cities along or near the east coast of the United States from the northern mid-Atlantic region to northern New England have been analyzed to determine if there are any weekly cycles in either daily precipitation frequency or intensity. Any such weekly cycle could be considered evidence of anthropogenic influence on the climate of that region. Data were examined for each individual site and for all sites combined. The data were subjected to various statistical procedures, including one-way analysis of variance, Student's t-test, and the chi-square goodness-of-fit test. Overall, results were not significant at the 95% confidence level. Thus, this study is unable to detect any weekly cycle in daily precipitation intensity or frequency.
This is all very interesting but our real job is to answer Michael's question.
References:
(1)David M. Schultz, 1998: Does It Rain More Often on Weekends? : Annals of Improbable Research, 4(2), 29.
(2) DeLisi, Mark P., Alan M. Cope, Jason K. Franklin, 2001: Weekly
Precipitation Cycles along the Northeast Corridor?. Weather and
Forecasting: Vol. 16, No. 3, pp. 343-353.
Prostate
cancer surgery found to cut death risk.
New York Times, 12 Sept. 2002, A16
Gina Kolata
Dilemma on prostate
cancer treatment splits experts.
New York Times, 17 September, 2002, F5
Gina Kolata
A randomized trial
comparing radical prostatectomy with watchful waiting in early prostate
cancer.
New England Journal of Medicine, Vo. 347, No. 11, September 12,
2002, 781-789
Lars Holmberg et al.
Looking at Steven Woloshin's table of health risks given in Chance News 11.03, we see that for men 70 or older who do not smoke, prostate cancer is the highest cancer risk for dying in the next ten years.
The issue of how a man who has been diagnosed to have prostate cancer should be treated has been highly controversial. Two standard choices are surgery, called randical prostatectomy to remove the cancerous prostate gland, and "watchful waiting." The argument against the operation has been that any operation has a risk and, in addition, the operation can result in incontinence or impotence. The argument agains watchful waiting is that the cancer will spread and become inoperable.
The articles by Gina Kolata deal with results announced in two NEJM articles reporting studies carried out in Sweden. The first article reports on a controlled experiment to compare the mortality rate due to prostate cancer for those who have the surgery and for those who choose watchful waiting. The second article reports the results of a follow up study to compare the "quality of life" for the two groups. We will discuss the first study.
For this study, from October 1989 to February 1999, 695 men with newly diagnosed prostate cancer were randomly assigned to watchful waiting or radical prostatectomy groups. 348 were assigned to the group to have the operation and 347 were assigned to watchful waiting. These subjects were followed through the year 2000. The primary end point was death due to prostate cancer, and secondary endpoints were overall mortality, the spread of the cancer, and the progression of the local tumor.
The follow up time had a median of 6.2 years. During the time of the study 31 of 348 assigned to watchful waiting died of prostate cancer, while only 16 of the 347 assigned to radical prostatectomy died of prostate cancer, representing a 50% reduction in the death rate from prostate cancer. Considering deaths from any cause, 62 of the 348 men in the watchful waiting group died and 53 in the radical prostatectomy group died.
The authors report that the decrease in death rate due to prostate cancer was significant (p = .02) while the death due to all causes was not significant (p = .3).
Here is a simple way to check significance. Assume that the surgery has no effect so that the chance of dying during the study is the same for the two groups. Then the 16 + 31 = 47 subjects in the watchful waiting group who died of prostate cancer would be equally likely to be in each group. Thus the subjects who died from prostate cancer that were in the watchful waiting group can be considered the result of tossing a coin 47 times and getting heads 31 times.
The expected number of heads in 47 tosses of a coin is 23.5 and the standard deviation is 3.43. The difference between the number of heads and the expected number is 31-23.5 = 7.5 which is 2.2 standard deviations. The probability of a deviation from the mean of this magnitude is p=.028 and hence significant at the .05 level Carrying out the same kind of computation for the overall deaths we find p = .4 so, as reported by the authors, the difference in the number due to all causes is not signficant.
The news articles made a big thing of the apparent puzzle that the operation caused a significant decrease in the death rate due to prostate cancer but not in the overall death rate. In her article "Dilemma on prostate cancer treatment splits experts," Gina Kolata asks a reader diagnosed with prostate cancer a series of questions to show the difficulty of making a decision. She writes:
Now, knowing that your likelihood of dying in the next six years is just the same, whether or not you have the surgery, but your likelihood of spending those six years impotent and incontinent is increased, do you still want the operation?
The authors of the paper and the press speculate how the operation could lower the chance of dying of prostate cancer but not the overall chance of dying.
It seems to us that the most likely explanation is that the study did not have the power to detect a significant difference in the death rate. To answer this question we investigate how sample sizes are determined for medical experiments of this type. Of course, the real answer is that they ask their SAS program or use formulas that appears in all books on clinical trials. However, the formula looked a little mysterious to us so we decided to see where it comes from. We found an elegant explanation by John Lachin in (1). We cannot resist giving it here though we realize that readers may want to skip this rather technical discussion.
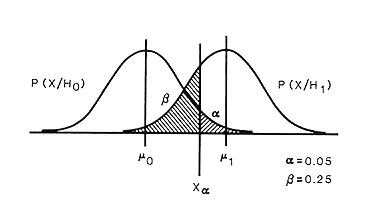
Lachin first considers the following general test of hypothesis problem. We have a statistic X that is normally distribution under null hypothesis Ho with mean mo and standard deviation s0 and under, an alternative hypothesis H1, it is normal with with mean m1 and standard deviation s1. We want to use the statistic X to accept or reject the null hypothesis. We specify a probability a for rejecting the null hypothesis when it is in fact true. In addition we specify a probability b of accepting the null hypothesis when H1 is the correct distribution for X.
Lachin provides the following picture that tells the whole story.
Here Xa = mo + Zas0 where Za is chosen to make P(X > Za) = a under the null hypothesis. Then if X < Xa we accept the null hypothesis and otherwise we reject it. Therefore the probability of a Type 1 error (false positive) is a. From the picture we see that that when X has has distribution specified by H1 we will accept the null hypothesis (Type 2 error, false negative) with probability b.
Now in clinical trials the distribution of X is determined by the sample n. We want to specify a, b and n so that we have the desired probabilities for errors of Type 1 and Type 2.
From our picture we see that the distance | m1 - m0 | is the sum of two parts, | Xa - mo| = Zas0 and |m1 - Xa|= Zbs1. Thus,
| m1 - m0 | = Zas0 + Zbs1.
Let's see how we can use this equation to find a formula for the sample size for the prostate cancer study.
We assume that, in each group, the number of deaths from prostate cancer can be considered the result of n Bernoulli trials with probabilities of death due to prostate cancer given by po for the watchful waiting group and p1 for the group that had the operation. From a previous study (2) the authors estimated that p0 = .11. They decided that if the operation caused a 6% decrease in the death rate from prostate cancer this would be considered "medically significant." Thus for the alternative hypothesis H1 they chose p1 = .05.
Let X be the difference between the proportion of deaths in the watchful waiting group and the group that had the operation. Then H0 is the hypothesis that p0= p1 and so m0 = 0. H1 is the hypothesis that p0 = .05 and since p0 = .11, m1 =.06. By the central limit theorem we can assume that under either hypothesis X is approximately normally distributed. To estimate the standard deviation of X under the null hypothesis we use p = (p0+ p1)/2 = .08 giving s1=Sqrt(2p(1-p)/n). Assuming H1, the standard deviation for the difference is s1= Sqrt((p0(1-p0)/n + p1(1-p1))/n). Thus our basic formula gives us:
| m1 - m0 | = Za Sqrt(2p(1-p)/n) + ZbSqrt((p0(1-p0) + p1(1-p1))/n).
putting in m1 - m0 = .06, p0= .05 and p1= .11, p = .08, Za = 1.645 and Zb= .842 and solving for n we obtain n = 320 for the number in each group. Therefore the authors choice of a total of 695 subjects has the desired power.
But does this number of subjects also give sufficient power to detect a similar difference in the overall death rate? To check this we shall estimate p0 by the proportion of deaths in the overall death rate of in this study. Recall that 62 of the 348 subjects in the watching waiting group died during the period of the study. This is a 17.8 % death rate. Thus again assuming that a 6% decrease in the death rate for the group having surgery is medically significant we will use p0= .178 and p1= .118. Putting these in our formula we find that now that we would need 549 for each group to have the same power that we had for death due to prostate cancer. So the study would have to have had over 1000 subjects to have at mosts a 20% chance of making a Type 2 error.
We can also use our basic formula to compute the power with 347 subjects in each group. Putting n = 347, p0= .178, p1= .118 and p = .148 in our formula and solving for Zb we find that Zb = .270. This means that there is 39% chance that you would accept the null hypothesis under hypothesis H1 which is almost twice the chance we had for death due to prostate cancer.
Since the time in the study differed for the subjects, the authors used the Kaplan- Meier method for survival analysis to obtain more detailed information. Here is their graph showing death rate from prostate cancer as a function of the number of years in the study.
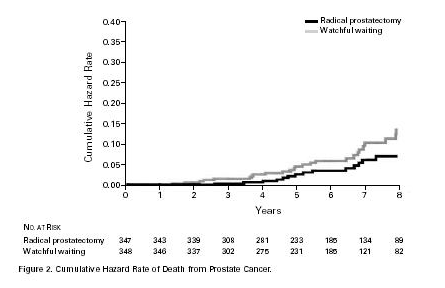
From this we see that the significant difference comes from those who were in the study at least five years.
See Chance News 10.06 for a discussion of how the Kaplan-Meyer method works.
References:
(1) "Introduction to sample size determination and power analysis for clinical trials", John M. Lachin, Controlled Clinical Trials 2, 93-113 (1981)
(2) Natural history of localised prostatic cancer, Johansson and others, The Lancet, 15 April, 1989, pp. 799-803.
DISCUSSION QUESTIONS:
(1) In their discussion of the sample size the authors write:
The initial target sample size was 520 patients. We planned two interim analyses, one after the enrollment of 300 patients and the other after the enrollment of 520. We decided to break the code and discuss the results in the steering committee if the P value was greater than 0.01 and less than or equal to 0.05 and to consider an early cessation for all patients if the P value was less than 0.01. In the interim analyses, none of the pre-stiplulated P values for breaking the code and revealing the results to the steering committee were reached; however, the overall mortality rate was lower than anticipated. Therefore, after the analysis of 520 patients, the target sample size was increased to 700 patients.
Do you see any problem with the change in design while the study is in progress?
(2) The lack of power for testing the overall death rate did not stop the experts from explaining why the overall death rate might not be signficantly different in the two groups even though death due to prostage cancer was. What do you think their explanations were?
Heads I win, tails you lose.
OR/MS Today, June 2002, p. 13
(Letter to the editor)
Francis J. Vasco and Dennis D. Newhart
It seems that we missed a Marilyn vos Savant story last spring! Vasco
and Newhart cite the following question from one of Marilyn's readers,
as presented in her March 31 column.
Say you're in a public library and a beautiful stranger strikes up
a conversation with you. She says, "Let's show pennies to each
other, either heads or tails. If we both show heads, I pay you $3. If
we both show tails I pay you $1. If they don't match, you pay me $2.
At this point, she is shushed. You think," With both heads one-quarter
of the time, I get $3. And with both tails one-quarter of the time,
I get $1. So half the time, I get $4. And with no matches half the time
she gets $4. So it's a fair game."
As the game is quiet, you can play in the library. But should you?
Should she?
Marilyn asserted that the stranger could win by showing twice as many
tails as heads (i.e., playing tails with probability 2/3 and heads with
probability 1/3), since this would provide an average gain of $1 for
every six plays. Not so, say Vasco and Newhart, who point out that the
opponent could then break even against her by playing all tails. As
they explain, what the stranger wins depends on the opponent's strategy.
They conclude that, "based on elementary game theory," the
stranger can win $1 on average every eight games no matter what her
opponent does by randomly playing heads with probability 3/8 and tails
with probability 5/8.
DISCUSSION QUESTIONS:
(1) Verify that playing all tails breaks even against Marilyn's proposed strategy. What was Marilyn assuming?
(2) Verify Vasco and Newhart's conclusion.
Ask Marilyn
Parade Magazine, 28 July, 2002, p 21
Marilyn vos Savant
Marilyn received the following letter:
My friend insists that the chances of any combination of six number being drawn in a lottery are identical. I contend that the chances of any sequence of six numbers (such as 1,2,3,4,5,6) being drawn are much higher. Who's right?
Bruce
Emery
Huntington Beach, Calif.
Marilyn answers:
You're both right. The chances of any one combination being drawn are identical to each other. But the chances of any sequence being drawn are higher (than the chances of any one combination), because so many sequences exist (such as 2,3,4,5,6,7). So you are comparing one combination of six numbers with all six-number sequences possibilities.
DISCUSSION QUESTION:
What was Bruce Emery trying to say and what did Marilyn mean by her answer?
Here is still another Marilyn problem for which she evidently wanted help from her readers:
Ask Marilyn.
Parade Magazine, 4 August, 2002, p 11
Marilyn vos Savant
Suppose you're on a game show. There are four boxes in an L-shaped configuration like this:
|
#1
|
|
|
#2
|
|
|
#3
|
#4
|
The host tells you: 1) One of the vertical boxes contains a chicken; and 2) one of the horizontal boxes contains a chicken. What are the chances that a chicken is in the corner box? In one way, the chances seem to be 1 in 3: but in another way, the chances seem to be 1 in 2. They can't both be right!
Toby Click, Macon, Ga.
Marilyn asks her readers to send her their answers.
DISCUSSION QUESTION:
What is the answer?
Michael Olinick sent us an interesting clipping from the "AP Off Beat" column in the Addison County (VT) Independent.
Jury with fewer surnames beginning with 'G' acquits
Florida man.
Addison County Independent, 27 July 2002, 3
Associated Press
'G' names in jury pool win suspect a new trial.
Miami Herald, 7 June 2002
Letter perfect: New jury finds ex-convict not guilty.
Miami Herald, 12 July 2002
Roderick Carter was being tried on gun charges in federal court in Miami.
Because he had a previous felony conviction, he was facing a severe
sentence. But his lawyer, David Markus, got him a new trial by arguing
that he had been denied the right to a jury of his peers. Carter is
black, and Markus maintained that Hispanics were overrepresented in
the jury pool.
The standard procedure for selecting jurors involved working alphabetically through the list. For Carter's trial, 21 of the 38 names in the jury pool started with 'G', and 14 of those were Hispanic. By contrast, there were only six blacks in the pool. The Miami Herald says that Markus "didn't use any sophisticated statistical analysis to bolster his point, just the phone book." In fact, the article reports that just five surnames--Garcia, Gomez, Gonzalez, Guerra and Gutierrez--account for more than half of the Miami residential listings under G.
While Markus may not be a statistical expert, he appears to have a literary bent. For rhetorical flourish he cited Shakespeare's Richard III in his argument. In the play, Richard, who is the youngest brother of King Edward, plots to gain the throne himself by arranging to have charges of treason brought against another brother, George--whose name starts with G. Alas, the articles provides no further detail as to how Markus drew the analogy with the present case.
Carter was acquitted at the new trial.
DISCUSSION QUESTION:
Here is the Shakespeare reference from which Markus argued:
Plots have I laid, inductions dangerous,
By drunken prophecies, libels, and dreams,
To set my brother Clarence and the king
In deadly hate the one against the other;
And if King Edward be as true and just
As I am subtle, false, and treacherous,
This day should Clarence closely be mewed up
About a prophecy which says that G
Of Edward's heirs the murderer shall be.
What do you think of the 'G' argument? Would it would be strengthened by a more "sophisticated" statistical argument?
Stochastic
Apportionment.
arXiv.org e-Print archive
Geoffrey Grimmett
In the U. S. Constitution a difficult mathematics problem, namely the apportionment problem is stated (but not solved). It is therein stated that "Representatives ... shall be apportioned among the several States ... according to their respective Numbers ... " It is relatively easy to give a mathematical description of the problem of apportioning the representatives. Suppose that there are r Representatives in the House, and there are s states, with populations a1, a2, ..., as. An exact apportionment would be to give the i'th state
qi = (ai/(a1 + a2 + ... + as)) r
Representatives. Of course, the problem is that qi is rarely an integer for even one value of i. So, the obvious way to proceed is to round qi up or down and use the resulting value bi instead. (Note that we have not described a procedure for obtaining bi.) An allocation is a vector of non-negative bi's whose sum is r. The allocation is said to satisfy quota if for each i, bi is less than one from qi (i. e. bi could be obtained from qi by rounding) and
b1 + b2 + ... + bs = r.
The basic question, to which answers have been given by many people over the past two hundred years, is what is the "fairest" way to obtain the bi's from the qi's. It must be added here that this question has been made more complicated in the case of the U. S. Constitution, because a further condition has been added, namely that none of the bi's should equal 0. It is fairly clear, by considering the example of three states with populations 1, 1, and 7, that it is possible that no allocation that satisfies quota exists with a lower bound of 1 on the bi's.
Over the years, Alexander Hamilton, Thomas Jefferson, and Daniel Webster all gave schemes for deciding how to obtain the bi's. The method that is currently in use in the United States was devised by a mathematician named Edward Huntington and a statistician named Joseph Hill. For a review of these methods, the reader is urged to consult Chance News, volume 10, number 2,
The paper under review proposes a completely new way to compute the bi's. The idea is to consider the bi's to be random variables which satisfy appropriate constraints (they are all non-negative and their sum is r). For a given state population distribution
(a1, a2, ..., as),
the collection B of bi's is called a random allocation. One can then ask whether a given random allocation "satisfies quota almost surely," i.e. if
P(B satisfies quota) = 1.
If an algorithm produces, for each state population distribution, a random allocation that satisfies quota almost surely, then the algorithm is said to satisfy quota. This paper gives an algorithm that satisfies quota, if there are no lower bounds. Here is the algorithm:
Step 1: Randomly permute the labels of the states. (Right here we can see that this would tax the brains of many of our politicians, so this algorithm probably cannot be used in this country.) The reason for this step is that the subsequent steps depend on the order of the states, "and it seems desirable to reduce to a minimum any correlations which depend on this extraneous element."
Step 2: Provisionally allocate the greatest integer of qi to state i. This leaves a certain number of unallocated seats. In fact, if we let q*i = qi - Floor(qi), then the number of unallocated seats is exactly r minus the sum of the q*i's.
Step 3: Let U be a (continuous) uniform random variable on [0, 1], and let
Qi = U + q*1 + q*2 + ... + q*i .
Let Ai be 0 or 1 depending upon whether the interval [Q(i-1), Qi) does not contain or does contain an integer. Then, for each i, allocate a further Ai seats to state i.
It is a nice (and relatively straightforward) probability exercise to show that this algorithm satisfies quota.
The paper also considers the case when positive lower bounds exist. In this case, it is possible that no algorithm exists that satisfies quota, so in order to come up with some sort of solution, one must relax the requirements of the problem. The new criterion is somewhat complicated and will not be given here. It is satisfying that under the relaxed requirements, an algorithm can be devised, and in fact, this algorithm reduces to the preceding one in the absence of lower bounds.
The paper concludes with some interesting data and history
of the allocation problem (as mentioned above, some of this is covered
in an earlier Chance News article).
DISCUSSION QUESTION:
Do you think that this method should be used for apportionment? If so do you think the supreme court would back it up if it was challenged?
Andrew Marlatt started his SatireWire site in December 1999 with 400 visitors a day and it has grown to a million visitors a day. It has been a one man show and his satirical articles have been enjoyed by millions and picked up by newspapers and journals. He has decided to call it quits. He will leave his site as an archive of satire. One might think this is like an opera singer who wants to quit while she is adored by her public but Andrew simply says "it has ceased to be fun." Here is a sample of his satire.
85 Percent of Nation's 2.9 Million Jobless
Say They're Not Just a Statistic
Washington, D.C. (SatireWire.com) — In a new Gallup poll on the dehumanizing aspects of job loss, nearly 85 percent of the nation's 2.96 million unemployed said they "agreed somewhat" or "agreed strongly" with the statement, "I am not just some mind-numbing statistic."
"I think what we found quite interesting was that the overwhelming majority of respondents, 75 percent, said they were genuinely hurt by efforts to categorize and compartmentalize their difficulties," said Gallup researcher Evan Krest. "This was particularly true of women between the ages of 30 and 49, and men who have been unemployed for six months or more."
But the most empirically moving answers, Krest added, were given by the 62 percent who said they hoped the study would finally put a human face on their anonymous plight.
"One 18-to-29-year-old woman said she was a real
person with a real name and real problems that could not possibly be
adequately conveyed using cold-blooded numbers," he recalled. "Unfortunately,
her responses were within the margin of error of plus- or minus-3 percent,
so she didn't count."
LaughLab
is an internet site that has dealt with the study of humor. It was created
by Dr. Richard Wiseman (University of Hertfordshire) in collaboration
with the British Association for the Advancement of Science. The aim
of this research was to find what kind of humor appeals to different
classes of people -- children, men vs. women, people living in different
countries etc. The site received more than 40,000 jokes and almost 2
million ratings. The study is finished and the results have been published
in a book "LaughLab." Here is the final winner:
A couple of New Jersey hunters are out in the woods when one of them
falls to the ground. He doesn't seem to be breathing, his eyes are rolled
back in his head.
The other guy whips out his cell phone and calls the emergency services.
He gasps to the operator: “My friend is dead! What can I do?”
The operator, in a calm soothing voice says: “Just take it easy.
I can help. First, let's make sure he's dead.”
There is a silence, then a shot is heard. The guy's voice comes back
on the line. He says: “OK, now what?"
Actually, we prefer the following joke that was in the lead at a previous announcement but ended up in second place:
Sherlock
Holmes and Dr. Watson go on a camping trip. After a good dinner and
a bottle of wine, they retire for the night, and go to sleep.
Some hours later, Holmes wakes up and nudges his faithful friend. "Watson,
look up at the sky and tell me what you see."
"I see millions and millions of stars, Holmes" replies Watson.
"And what do you deduce from that?"
Watson ponders for a minute.
"Well, astronomically, it tells me that there are millions of galaxies
and potentially billions of planets. Astrologically, I observe that
Saturn is in Leo. Horologically, I deduce that the time is approximately
a quarter past three. Meteorologically, I suspect that we will have
a beautiful day tomorrow. Theologically, I can see that God is all powerful,
and that we are a small and insignificant part of the universe. What
does it tell you, Holmes?"
Holmes is silent for a moment. "Watson, you idiot!" he says.
"Someone has stolen our tent!"
Not surprisingly the favorite joke for the USA is a golf joke.
A man and a friend are playing golf one day at their local golf course. One of the guys is about to chip onto the green when he sees a long funeral procession on the road next to the course. He stops in mid-swing, takes off his golf cap, closes his eyes, and bows down in prayer. His friend says: “Wow, that is the most thoughtful and touching thing I have ever seen. You truly are a kind man.” The man then replies: “Yeah, well we were married 35 years.”
You can find the favorite jokes at a number of other countries on the LaughLab web site. You can also find differences in joke appreciation in different countries. Wiseman says::
We asked everyone participating in LaughLab to tell us which country they were from. We analyzed the data from the ten countries that rated the highest number of jokes. The following ‘league table’ lists the countries, in the order of how funny they found the jokes:
Most funny
|
Germany France Denmark UK Australia The Republic of Ireland Belgium USA New Zealand Canada |
And you will be able to read the book "Laughlab: The Scientific Search for the World's Funniest Joke" when it comes out in December 2002.
Stan Selzer suggested following topic.
Supreme Court of the United States
Utah
et al. v. Evans, Secretary of Commerce, et al.
Supreme Court of the United States October 2001 session
As in previous censuses, the 2000 census employed the method of "imputation" by which it infers that the address or unit about which it is uncertain has the same population characteristics as one of its geographic neighbors of the same type.
In the 2000 census the use of imputation increased the population by about .4%. Of course, this was not evenly distributed between states and Utah's population was increased by imputation by only .2% while North Carolina's was increased .4%. This caused North Carolina to receive one more Representative and Utah one less than would have been the case if imputation had not been employed.
The Census Act prohibits the uses of statistical sampling to determine the population for congressional apportionment purposes. The Census Act was modified by congress to allow sampling in all areas except to determine the population for apportionment purposes. In 1999 the Supreme Court ruled this implied that sampling to adjust for the undercount could not be used for apportionment.
Based on this ruling, Utah challenged in the courts the use of imputation for apportionment purposes arguing that it is a form of sampling. This challenge reached the Supreme Court in the October 2001 session. The Supreme Court voted 5 to 4 against Utah.
The summer meetings of the American Statistical Association had a panel discussion on what was learned from this ruling. The panel consisted of four statisticians who has testified for this Supreme Court case: Lara Wolfson, Brigham Young University, Donald B. Rubin, Harvard, Joseph Waksberg, Westat Research Corporation, Howard Hogan, the Census Bureau. The first two argued that imputation was sampling and the second two argued that it was not.
Lara Wolfson and Donald Ruben argued that the imputation process was a form of sampling since observations from a subset of the population are being used to draw inference about the unobserved population, and hence, of the population as a whole.
They further argued that, since the sampling proposed for the undercount problem ruled out by the 1999 Supreme Court decision relied on randomly selected household units in a nonresponding tract and imputation sampling did not use random sampling, there was even a greater argument for ruling out imputation sampling.
Joseph Waksberg argued that imputation should be compared to nonresponse in surveys, and in the survey literature nonresponse and adjustments for their effects are described as methods that are distinct from the sampling operations. He comments that there have been major statistical conferences devoted to nonsampling problems in surveys and censuses that included discussions of imputation and other methods of compensating for missing data.
Howard Hogan argued that the definitions of Wolfson and Ruben do not make clear that, in sampling, the process of selecting a sample is a deliberate and purposeful activity occurring during the design phase of a survey.
He argued that imputation is not a method for selecting units during the design phase of a census or sample survey but rather is a means of dealing with missing data in the data processing stage.
Lara Wolfson was the chief statistician for the state of Utah in this case and in a previous case where Utah challenged the census policy of counting members of the military personal and federal employees serving outside the United States and not counting other Americans living outside the country. Not counting any such Americans would also have allowed Utah to keep its 4 representatives.
To us the most interesting part of the discussion was Wolsfon's account of what it was like to be working on a case before the Supreme Court. Fortunately, she and Thomas Lee, lead counsel for Utah in their two lawsuits, have written this story for Chance Magazine and you will be able to read it there.
Readers will also enjoy reading the the Supreme Court decision itself.
It provides an interesting insight into how the Supreme Court makes
decisions in the context of an issue of interest to us and our students.
Unlike most recent 5 to 4 rulings you will have a hard time guessing
who the 5 were.
We leave this to our readers to read but cannot resist showing that even the Supreme Court prizes the value of a good example. The majority opinion writes:
Imagine a librarian who wishes to determine the total number of books in a library.
If the librarian finds a statistically sound way to select a sample (e.g., the books contained on every 10th shelf) and if the librarian then uses a statistically sound method of extrapolating from the part to the whole (e.g., multiplying by 10), then the librarian has determined the total number of books by using the statistical method known as “sampling.”
If, however, the librarian simply tries to count every
book one by one, the librarian has not used sampling. Nor does the latter
process suddenly become “sampling” simply because the librarian,
finding empty shelf spaces, “imputes” to that empty shelf
space the number of books (currently in use) that likely filled them—not
even if the librarian goes about the imputation process in a rather
technical way, say by measuring the size of nearby books and dividing
the length of each empty shelf space by a number representing the average
size of nearby books on the same shelf.
This example is relevant here both in the similarities and in the differences that it suggests between sampling and imputation.
The opinion then goes on to explain what they consider the similarities and differences to be.
DISCUSSION QUESTIONS:
(1) If you were asked to testify before the Supreme Court which side would you have supported? What arguments would you give?
(2) Do you think it is possible to give a definition of sampling or is it just a semantics game?
Bob Johnson wrote to us that the 6th annual Beyond the Formula Conference was a great success and that he is making an arhive for this conference on their web site.
We asked André Lubecke, who attended the conference, to write her impressions of the conference. She said she would give us some of her notes and we could see if we could make a report from these. However, we felt that her notes gave a fine snapshot of the conference and we did not want to mess them up so here they are:
Notes on Beyond the Formula Conference.
August 8-9, Monroe Community College in Rochester, New York
Andre Lubecke
Keynote Address and Closing remarks – Joan Garfield
- Focus on the Big Ideas : variability, model, distribution, association
- Revisit them often because they are “fragile”
- Some difficulties students have that have been documented: we use
words and symbols with which they are already familiar BUT we use them
in new ways; context can be misleading; misconception that stats is
math; statistical reasoning is difficult
“Multimedia For Teaching Introductory Statistics” Paul Vellman’s
Talk
- Three rules of data analysis
- Make a picture – to think
- Make a picture – to explore
- Make a picture – to explain
- Introduce only one new idea at a time and connect it to something
(He gave his proposed ordering of material)
- We’ve taken over the alphabets by the end of the semester:
Z, t, P, p, s, F, n, q, a, b, r, s,
- Always check assumptions and conditions
- Always check plausibility of answers, especially if gotten through
technology
At all other time slots there were excellent speakers and interesting
topics opposite each other and it was very difficult to choose which
ones to attend!
Beth Chance, Allan Rossman, and John Spurrier all did multiple presentations
on classroom activities .
There were multiple sessions on various aspects of AP Statistics and
a number on topics in assessment.
There were a few sessions designed for attendees to interact on some
issues in education through debate and discussion.
The organizers did a wonderful job and the food was excellent. (Lunches and a dinner were provided.) Florence Nightengale came to dinner.
I found Rochester very interesting. The river ran alongside my hotel.
During one of the sessions I attended, I learned how a market research
company gathered information to support a nationwide product launch.
We learned how they decided to whom to send samples of the product in
order to determine target populations and potential customer response.
During another I learned a way to determine how many suitors I should
let go by in order to maximize my chance of finding my Prince Charming.
Copyright (c) 2002 Laurie Snell
This work is freely redistributable under the terms of the GNU
General Public License published
by the Free Software Foundation.
This work comes with ABSOLUTELY NO WARRANTY.
CHANCE News 11.04
13 July 2002 to 10 October 2002