!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

      CHANCE News 10.06

         May 21, 2001 to July 4, 2001

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Prepared by J. Laurie Snell, Bill Peterson, Jeanne Albert, and Charles Grinstead, with help from Fuxing Hou and Joan Snell.

We are now using a listserv to send out Chance News. You can sign on or off or change your address at this Chance listserv.This listserv is used only for mailing and not for comments on Chance News. We do appreciate comments and suggestions for new articles. Please send these to:

jlsnell@dartmouth.edu

Back issues of Chance News and other materials for teaching a Chance course are available from the Chance web site.

Chance News is distributed under the GNU General Public License (so-called 'copyleft'). See the end of the newsletter for details.

Is this the earliest reference to such an observation?

Speaking of origins of quotes, a member of the Science Writer listserv asked if anyone knew the actual quote from Einstein regarding God does not role dice? Another member replied:

                            ====================================================
                                             When the Okies migrated from Oklahoma to California,
                                              they raised the average IQ's of both states.
                                                                                                         
                                                                                                             Will Rogers
                           ====================================================

Does anyone know a reference for this quote?

                                    <<<========<< >>>>>

 

==============>
Here are two Forsooth items from the May 2001 issue of RSS News.

>>>>>=============>
John Paulos noticed a Forsooth item in a recent column of William Safire. Safire assumes that Bush will run in 2004 and gives his odds for each of 10 possible democratic presidential candidates being Bush's opponent. John observes that his odds give a probability of 168% that one of the ten will be Bush's opposition. You can find Safire's column and John's commentary here.

Our readers would also enjoy Paulos' June and July ABC news columns. In his June column John discusses Simpson's paradox and a course load paradox. In his July column he gives an interesting explanation for why the correlation of SAT scores to freshman grades appears to be lower than it actually is.
                                        <<<========<<


>>>>>=============>
Ask Marilyn.
Parade Magazine, 27 May 2001, 16
Marilyn vos Savant

A reader writes: "My husband flies at least 100 times a year. I know the odds of an accident are the same for every flight, but I say he is more likely to be involved in one than someone who flies less. He insists this in not an actual risk for him."

Marilyn responds "I agree with both of you. If your husband flies 100 times a year, he runs 100 times the risk of someone who flies only once a year. But his risk is still statistically insignificant. Flying is amazingly safe."

DISCUSSION QUESTIONS:

(1) In Chance News 8.09, we summarized Arnold Barnett's Chance Video lecture "Risks in Everyday Life," which estimated the risk of death by flying to be about 1 in 7 million. Consider taking 100 flights, each of which exposes you to this risk. Marilyn's argument suggests that your cumulative risk is 1 in 70 thousand. Is this approximately correct? What assumptions are you making?

(2) What do you think Marilyn means by the phrase "statistically insignificant"? Suppose someone flies 100 times a year over a 30-year career. Would you characterize this person's cumulative risk as "statistically insignificant"?

(3) How reasonable is it to assume that "the odds of an accident are the same for every flight?"
                                         <<<========<<



>>>>>=============>
Glass floor : How colleges reject the top applicants--and boost their status.
The Wall Street Journal, 29 May 2001, A1
Daniel Golden

In the "old days," according to this story, colleges accepted the applicants with the best credentials, and wait-listed the less well-prepared. In the last decade, a new trend has emerged. Applicants perceived as "overqualified", and thus likely to choose other institutions, have been placed on the waiting list, while admission is offered to students who are objectively less qualified but more likely to enroll. This practice has become especially common among schools perceived as just below the top tier. The article begins with the example of Franklin and Marshall College in Pennsylvania, which last year rejected 140 of its top applicants. These students had not interviewed with the school or otherwise shown real interest in attending, and past admissions experience suggested that they were not likely to enroll.

Are such schools just being realistic, or are they playing a numbers game with their admissions scores? That is the question raised by the article, which points out that acceptance rate and admissions "yield" (the percentage of those admitted who ultimately enroll) counts for 1/4 of the selectivity score in the popular US News College Rankings. The article estimates that changes in these numbers could move a school up or down several positions in the rankings. Emory University in Atlanta, often used as a back-up school by Ivy League applicants, is cited as a big winner in efforts to improve yield. Over the last ten years, Emory has improved its yield from 23% to 33% by giving preference to candidates who visit the campus, interview with the school, or meet with representatives at college fairs.

There is no question that colleges are receiving more applications each year, owing in part to increasing national competition for admission. To manage the process, schools are turning to admissions consulting firms, who apply sophisticated statistical models that use intended major, extracurricular activities, and other demographic variables to predict the chance that an applicant will enroll if accepted. In some of these models, when an applicant's test scores exceed the median for the school, the predicted chance of enrolling goes down.

The new policies may have some unfortunate side effects. A highly qualified applicant who is not accepted at a top-ranked school may find herself also rejected by the second-tier schools who perceive her as overqualified. According to the article, colleges are now getting angry phone calls from parents and guidance counselors of students stranded in this strange new middle ground.

DISCUSSION QUESTIONS:

(1) How do you think the article estimated the effect of yield on the position in the US News ranks? You can find more detail about the formula on the US News web site.

(2) Besides improving the yield numbers, what other benefits can you see to the strategy favoring applicants with demonstrated interest in the school? Can you think of any other risks?
                                        <<<========<<



>>>>>=============>
Placebo Placebo effect is more myth than science, study says.
The New York Times, 24 May 2001, A20
Gina Kolata

Is the placebo powerless? An analysis of clinical trials comparing placebo with no treatment.
New England Journal of Medicine, 344 (24 May 2001): 1594-1602.
Asbjorn Hrobjartsson and Peter C. Gotzsche

The powerful placebo and the Wizard of Oz.
New England Journal of Medicine, 344 (24 May 2001): 1594-1602.
John C. Bailar III

The use of placebo controls in randomized experiments is familiar to all students of statistics. A more radical use of placebo was advocated in a New York Times Magazine article entitled "The Placebo Prescription," which we summarized for Chance News 9.02. The central idea there was that the placebo effect observed in clinical trials could be harnessed as a legitimate medical treatment. But now two Danish researchers have reported in the New England Journal of Medicine that the therapeutic value of placebos is essentially a myth.

Dr. Hrobjartsson is quoted in the New York Times as observing that no published research had made the distinction between the placebo effect and the natural variations in symptoms as a disease runs its course. He and his colleague, Dr. Gotzsche, therefore undertook an extensive literature review to find studies which included both a placebo group and an untreated group. If the placebo effect is real, they reasoned, then it ought to show up in comparisons of the placebo group with the untreated group. Ultimately, they identified 114 suitable studies, involving a total of 7500 patients and 40 different medical conditions.

A number of categories of studies had to be distinguished. Some involved binary responses (the patient's condition either improved or did not), while others had continuous responses. In some, the response was based on the patients' subjective perceptions, whereas others measured physiological responses. Also, three types of placebos were distinguished: pharmacological (such as pills), physical (such as manipulation), and psychological (such as a conversation).

For binary outcomes, there was no significant difference between placebo and no treatment. Considering subjective and objective responses separately gave results similar to the overall results. On the other hand, for continuous outcomes there was a significant difference overall between placebo and no treatment groups. However, when the continuous results were broken down by response type, the subjective responses showed a significant difference, while the objective responses did not. Furthermore, it was found that the effect decreased as the size of the trials increased. The researchers suggested a possible bias in the smaller trials: the patients' subjective reports of improvement in smaller studies may reflect a desire to please their doctors. Patterns similar to the above were observed when pharmacological, physical and psychological placebos were considered separately.

Hrobjartsson and Gotzsche conclude that placebo treatment has no use beyond clinical trials experiments. In an editorial accompanying the research article, John Bailar compares the power of the placebo to the power of the Wizard of Oz, which depended on no one looking behind the curtain. Still, Bailar seems uncomfortable with a complete rejection of placebos. While he calls for careful scrutiny of any proposed uses, he holds out some hope that they may still be useful in specific settings, such as pain relief.

The New York Times article presents interesting observations from other experts. We read: Dr. Donald Berry, a statistician at the M. D. Anderson Cancer Center in Houston, said

referring to a well- known statistical observation that a patient who feels particularly terrible one day will almost invariably feel better the next day, no matter what is done no matter what is done for him.

On the other hand, Berkeley statistician David Freedman pointed out that pooling data from many studies in a meta-analysis can sometimes produce misleading results. He is quoted as saying:

I just don't find this report to be very persuasive.
The evidence of a placebo effect is maybe a bit less
than I thought it was, but I think there is a big effect
in many circumstances.

DISCUSSION QUESTIONS:

(1) Tom Wallsten suggest that the New York Times remarks about what Donald Berry said should be considered for a Forsooth item. What did he have in mind?

(2) Freedman, and also Bailar to some extent, appear to be arguing that placebos might work in specific settings, even if no general "placebo effect" turns up in a comprehensive examination of all applications. Do you agree? How do you think Hrobjartsson and Gotzsche might respond?

(3) In his editorial, Bailar notes that "...the research setting, with its generally intense methods of observation and precise measurement of outcomes, may obscure a real effect of placebo that would be evident in nonresearch settings. However, it is not clear how one could study and compare the effects of placebo in research and nonresearch settings, since that would of course require a research study." Do you see any way out of this paradox?
                                         <<<========<<



>>>>>=============>
Connoisseurs of Chaos Offer A Valuable Product: Randomness.
New York Times 12 June, 2001
George Johnson

Randomness as a resource.
American Scientist, July-August 2001
Brian Hayes

These are two excellent articles on how random numbers have used and how they have been generated from the past to the present. As we learn from the Times article, there is a long history to ways to generate random sequences. Weldon tried rolling dice but then Karl Pearson showed that there to be too many 5's and 6's. A similar problem occurred when Tippetts tried to randomly select numbers from a bag with a thousand cards. Fisher and Yates used two decks of playing cards and again there were too many sixes. Then came the publication of "A million random numbers" by Rand Corpration. Finally, the computer produced pseudo-random numbers. While statisticians were experimenting, mathematicians were trying to give a mathematical definition of a random sequence. After many failures there appears to be some satisfaction with the modern Chaitin-Kolmogorov defintion which states that a sequence is random if the length of the shortest program to produce the first n digits is essentially as long as the n digit sequence itself. But by their definition any sequence that you can produce by an algorithm which includes pseudo-random sequences cannot be random. Thus someone who really needs truly random sequences has to turn elsewhere.

If we believe in quantum physics, the natural place to turn is nature itself. The Times article discusses three web sites that will produce random sequences for you by physical processes. The first site Hotbits generates random digits by using radioactive decay. The second site Random.org uses a radio tuned between stations to obtain atmospheric noise. The third site called Lavarand is based on the idea that a lava lamp is a chaotic system. Each of these sites has a good explanation of how their system works. Random.org has a general discussion of random numbers and links to other sites that provide such information.

None of these web solutions are yet able to produce large numbers of random sequences fast enough for many of the simulations we are used to carrying out. However, according to the American Scientist article, there are hardware solutions that produce random numbers using thermal noise that can be plugged into your computer. Also such a generator is part of the newer Intel Pentium processors.

The American Scientist article has more details on some of the modern applications of random numbers especially in the field of cryptography.

DISCUSSION QUESTION:

Even sequences that are produced by physical processes sometimes fail to pass statistical tests and have to be modified by mathematical methods. For example, from the FAQ page of the Random.org site we read:

A digital camera takes a picture of some Lava Lite lamps, the digital output
of that image is fed into various number mungers and kablam! you have a
bona fide random number.

Why do you think the number mungers are necessary? Do you think this is cheating?
                                      <<<========<<



>>>>>=============>
Mike Olinick suggested the following story.

Group seeks moratorium on federal executions; Bush administration accused of stalling study on racial bias as date nears for inmate Garza.
The Washington Post, 4 June 2001, A2
William Claiborne

U.S. death penalty system not biased, Ashcroft declares; Study finds disparities in prosecution.
The Washington Post, 7 June 2001, A29
Dan Eggen

Opponents of the death penalty charge that its imposition in federal cases reflects racial and geographical biases. Fourteen of the twenty prisoners now on federal death row are minorities, and the majority of death penalty cases arise in conservative states. The advocacy group, Citizens for a Moratorium on Federal Executions, is asking that all federal executions be put on hold until these problems can be further investigated.

The issue is pressing because a Mexican-American inmate, Juan Raul Garza, is scheduled to be executed on June 14 for his role in several murders related to drug-trafficking. The first article presents the Citizens group's charge that the Bush administration is delaying the release of a pending death penalty study in order to expedite Garza's execution. The study was begun by Attorney General Janet Reno during the Clinton administration, and President Clinton had granted Garza a stay of execution while the study was being conducted.

By the time of the second article, the study had been released. Attorney General John Ashcroft maintained that it shows no evidence of racial bias. Echoing statements made by George W. Bush in defense of the Texas death penalty, Ashcroft asserted that there is no doubt about the guilt of any of the current federal death row inmates. He also pointed out that blacks and Hispanics are less likely than whites to face capital punishment after being charged. But critics counter that minorities are more likely to be charged with capital crimes in the first place, and that this disparity leads to the preponderance of minorities on death row.

The study did find that whites were more than twice as likely as blacks to avoid the death penalty through plea bargains. While conceding that such bargains might need more careful attention in the future, Ashcroft tried to downplay the finding as a "minor statistical discrepancy."

Bruce Gilchrist, who is one of Garza's attorneys, still feels that the study has been released too late to help in appeals for his client. Moreover, he adds that the study fails to provide any real insight into what is going wrong with the system. Further concerns from the Garza defense team are presented in a recent New York Times article ("Lawyers trying to stop execution cite flaws in bias report," 13 June, 2001, A24). There they criticize the study for ignoring potential death penalty cases in which the death penalty was not sought.

DISCUSSION QUESTIONS:

(1) The New York Times article summarizes the study's findings by saying that "in nearly 80 percent of the cases in which prosecutors sought the death penalty, the defendant was a member of a minority group and nearly 40 percent of death penalty cases originated in nine of the states." Does the second figure necessarily show geographical bias? What else would you like to know?

(2) If 80 percent of capital cases have a minority defendant, can it still be true, as Ashcroft, asserts, that blacks and Hispanics are less likely to face capital punishment after being charged?
                                        <<<========<<



>>>>>=============>
We read three new books that will be of interest to your readers. The first is sure to make you feel better about statistics but then the other two might make you feel worse.

The Lady Tasting Tea : How statistics revolutionized science in the twentieth century.
W H Freeman & Co. May 2001
David Salsburg

David Salsburg is a statistician who has retired from a career which combined teaching in several colleges and universities and doing research for the Pfizer pharmaceutical company. He has written a lively popular account of the development of twentieth century statistics. The leading actor in the book, not surprisingly, is R. A. Fisher.

Salsburg combines a discussion of the how the basic statistical concepts were developed along with a story of the lives of the statisticians who developed them. Reading the book, one is reminded what an interesting group of scientists this was, including Sir Ronald Fisher, Karl Pearson, Sir Francis Galton, William (Student) Gosset, Egon Pearson, Jersy Neyman, Jimmy Savage, Andrei Kolmogorov, Florence Nightingale, William Feller, Samuel Wilks, John Tukey, Edward Deming and Box and Cox. As you read about the giants of the field arguing about what are the correct number of degrees of freedom, what does significance mean, what are p values, and can you test a hypothesis without an alternative hypothesis, you wonder when they will make the movie.

Reading this book one can appreciate a remark made by Brad Efron on its cover:

                  If scientists were judged by their influence on science, then Fisher would
                  rank with Einstein and Pauling at the top of the modern ladder.

One can also appreciate that Fisher's success was due, in no small degree, to his deep understanding of several different fields including mathematics and genetics.

The story of Tukey, responding to the war effort and giving up his already impressive work in abstract mathematics in topology to work on statistics, is but one example of the enormous effect World War II had on the development of statistics. Of course the Deming story is another.

To make his characters come to life Salsburg has used stories he learned from interviews with others who were there. He also acknowledges help from the fine series of interviews with statisticians that has appeared in Statistical Science.

One problem with relying on interviews is that people's memories are not so reliable sometimes. This leads to a number of small errors such as: Fisher didn't propose testing the lady's ability to tell whether the milk was put in first or not, it was Wiliam Roach (assuming we believe Joan Fisher Box), Feller's first job when he came to America was not at Princeton but rather at Brown, and Ville, not Levy, was the first to use the word Martingale for a chance process. But who cares? Its the story that we want and Salsbury tells a great story!
                                            <<<========<<



>>>>>=============>
Damned Lies and Statistics: untangling numbers from the media, politicians and activists.
University of California Press, May 2001
Joel Best

It Ain't Necessarily So : How media make and unmake the scientific picture of reality.
Rowman & Littlefield; April 2001
David Murray, Joel Schwartz, and S. Robert Lichter

We are sure that methods for lying with statistics were well known to the Greeks, but the art of doing so was first popularized in modern times by the charming book How to lie with statistics by Darrell Huff. More recently we have had Cynthia Crossen's wonderful book Tainted Truth , which told us how statistics gets contaminated when sponsored by industries, especially pharmaceutical companies.

Now we have two new books that tell us how easy it is to mangle statistics related to public policy decisions such as AIDS, Gun laws, domestic violence, and the census. These two books are remarkably similar and you can hear the two authors amiably discussing their books on NPR Science Friday. June 08, 2001.

Joel Best, author of "Damned Lies and Statistics," is professor of criminal justice at the University of Deleware. "It Ain't Necessarily So" has three authors, Murray, Schwartz and Lichter.. David Murray is director of of the statistical assessment service (STATS) and adjunct professor at Georgetown University. STATS publishes the monthly newsletter Vital STATS which, like Chance News, discusses statistical issues in the news. You might like to look at the June issue where you will find a discussion of the placebo study mentioned above and several other interesting current articles that we have not discussed. Joel Schwartz is senior adjunct fellow at the Hastings Institute, and S. Robert Lichter is president of the Center for Media and Public Affairs in Washington and also of STATS.

The main difference between these two books is one of emphasis. Like Crossen, Best emphasizes that problems arise from the fact that those who produce data for policy issues typically do so because they want to use them to support a particular political position. Murray and his co-authors emphasize problems that arise when the news media transmits the information to the public.

Both books identify several basic kinds of errors commonly made and then discuss these in the context of recent studies or news reports. We consider first Best's book.

The Introduction discusses the author's candidate for the the worst social statistical social statistic ever: Every year since 1950, the number of American children gunned down has doubled. Chapter 1 discusses the importance of social statistics. The remaining chapters treat specific kinds of problems.

Chapter 2 is titled Soft Facts. An example of a soft fact is: an activist reports on Ted Koppel's program that there are 2 or 3 million homeless, this is a ball park figure or possibly even just a guestimate. The number then takes on a life of its own and is soon treated as an established fact.

Chapter 3 is titled Mutant Statistics. Here is an example of a mutant statistics: the FBI reports that in homicide cases, 15 percent of the victims and offenders are strangers, while nearly 40 percent of the victim-offender relationships are unknown. This statistics is "mutated" when an advocate assumes that if the FBI cannot tell the relationship it must be that of a stranger. This increases the estimate of the number of offenders who are strangers from 15% to 65%.

Chapter 4 is called Apples and Oranges. An example is the comparison of arrest rates by race rather than by economic or social status.

Chapter 5 is titled Stat wars. A stat war was started when estimates were made of the number of people who attended the 1995 Million-Men March in the Capital Mall led by Louis Farrakan. The leaders wanted a large number to show their success and the Park officials wanted a number that they felt was closer to reality. The war resulted in Congress instructing the Park officials to no longer give estimates of crowd sizes in the Mall.

Chapter 6 is titled Thinking about Social Statistics. In this chapter the author encourages the reader to use the author's classification and examples to develop a check list that should go through the reader's mind when reading reports of statistics related to policy questions.

We turn now to "It Ain't Necessarily So." After an introduction, Making news and making sense, the book is divided into three parts: Part 1: The ambiguity of news, Part 2: The ambiguity of measurement, and Part 3 "The ambiguity of explanation. Each part contains several examples from major newspapers to illustrate the ambiguities that the authors have in mind.

One of the authors' examples of t he ambiguity of news is: In February 1996 the New York Times and Washington Post gave good coverage when the CDC had bad news about the spread of Aids. But in April 1996 when the CDC had some news that on-the-whole was good news, the Post and Times chose to emphasize the bad part of the news. Other examples are given to support the theory that the media has a tendency to prefer writing about bad news rather than good news. The authors also feel that the news media -- even the New York Times-- not only print news that is fit to print but also news that is not fit to print. This can result, for example, from a public relations campaign, designed to sell a book. They suggest that this was the case when all the major newspapers reported that sperm counts are falling based on very flimsy evidence.

Examples of the ambiguity of measurement occur often when the media reports news on the extent of domestic abuse, rapes, and family abductions. Those responsible for official estimates use technical definitions which often are not consistent with more informal definitions understood by the public and used in surveys and reported in the news. Other ambiguities arise from using proxies. For example, a report of the National Research Council suggests that much of the news about the danger of electromagnetic forces was flawed because it was based on wrongly equating proximity to power lines with exposure to EMF's. Similar problems occur with attempts to measure income as a proxy for poverty or what people say on surveys as a proxy for hunger. Other examples of ambiguities are given that arise from contradictory surveys, different methods for measuring risk and changes in ways of measuring a particular phenomena. An example of the latter is a report that the crime rate is up. This might simply be the result of improved ways to track the incidence of crime.

The authors begin their discussion of "The ambiguity of explanation" by remarking how easy it is for motives to effect interpolations of studies. For example, environmentalists tend to ignore the work of those who doubt that global warming is a serious threat, The authors discuss effective peer review as a way to assure unbiased results. They point out that researchers, referees, and editors are certainly not immune to having biases. Another ambiguity of explanation is the tendency to accept the obvious explanation when less obvious explanations may be closer to the truth. For example, the Census Bureau reported that income inequality had been growing steadily since 1968. It was natural to attribute this primarily to changes in the economy as appeared in a front page story in the New York Times. However, the Census bureau itself advanced both economic and demographic explanations. While the Times mentioned some demographic issues, the main emphasis was on the economic issues.

The authors of both books emphasize that almost anyone who uses statistics to support a public policy has his own political agenda. And it is also natural to ask how much does bias affect these authors' critiques. In a review of "It Ain't Necessarily So" in Salon, July 2, 200, writer David Appell argues that the authors' conservative backgrounds lead to biased discussions of the the way news is reported, especially those new items relating to issues where conservatives have an active interest. Appell chooses, as an example, the authors' criticism of the coverage of a study of Camille Parmesan's reported in "Nature" in August 1996. This was a study of the extinction rates of local populations of a western butterfly, the Edith's checkerspot. Parmesan observed that, overall, the butterfly had moved north by about one hundred miles and suggested that this was evidence of global warming. Appell makes a pretty good argument that the critique is biased but then maybe he's a flaming liberal! However, we always say that "you should look at the data." So, since almost all the articles discussed in the book are available from Lexis Nexis, readers of "It Ain't Necessarily So" might enjoy reading the news articles along with the critiques to make up their own minds.

One small suggestion of newspapers' bias that the authors could not include in their book is that the Los Angeles Times, New York Times, and Boston Globe have all gave excellent reviews of "Damn Lies and Statistics" books, but so far none has reviewed "It Ain't Necessarily So."

Throughout his book, Best stresses that the public really has much too much faith in numbers. The public seems to feel that the mere appearance of numbers in an argument for a public policy makes the argument more convincing. Best further observes that, in the social sciences, it is rare to have an exact number. In a recent New York Times article ("Truths, half-truths and the census, 1 July 2000, Janny Scott", Kenneth Pruit, former director of the Census Bureau, calls the census "estimates of the truth." According to the article:

Mr. Prewitt wistfully suggests a nationwide numeracy campaign. The
country talks about improving literacy, he says. But most of the public
conversation is about numbers: statistics,trend lines, social indicators.
Perhaps the country should take numeracy as seriously as literacy if it
wants intelligent public discourse.

These books should make a significant contributions to statistical literacy.

DISCUSSION QUESTIONS:

(1) How do you feel about the way the news handles statistics related to public policy issues. Can you give good and bad examples?

(2) If you were advising an editor of a newspaper on how to improve their reporting of statistical data what would you recommend?
                                       <<<========<<



>>>>>=============>
We usually do not go into the technical details of a study that we discuss in Chance News but decided that it might be fun to try this. We chose the study "Survival in academy award-winning actors and actresses," Annals of Internal Medicine, Vol. 134, No. 10, by Donald A Redelmeir and Sheldon M. Singh discussed in Chance News 10.05. Redelmeier was also the lead author of the interesting study on the danger of using a cell phone while driving, discussed in Chance News 6.03 and 6.10 and in an article "Using a car phone like driving drunk?" in Chance Magazine, Spring 1997.

Recall that for their Oscar study the authors identified all the actors and actresses who had been nominated for an award for leading or supporting role since the Oscar awards were started 72 years ago. For each of them, they identified another cast member of the same gender in the same film and born in the same era. This provided a group of 887 actors to be used as a control group for their study of Oscar winners. From those nominated there were 235 Oscar winners. The authors wanted to determine if Oscar winners tend to live longer than comparable actor who were not winners. Thus the key question is how do you decide if there is a significant difference in the life expectancy of members of two different groups.

A similar problem arises in a medical trial in which one group of patients is given a new treatment and a second group is given a placebo or a standard treatment and the researchers are interested in the expected time until a particular "end event" occurs such as death, the disappearance of a tumor, the occurrence of a heart attack etc. The test that is generally used for such studies, and was used in the Oscar study, is called the "Kaplan-Meier survival test". This test was developed by Kaplan and Meier in 1958 ("Nonparametric Estimation from Incomplete Observations," Journal of the American Statistical Association, Vol. 53, No 282, 457-481). The importance of this test is suggested by the fact that Science Index shows that over 22,000 papers have cited the 1958 Kaplan and Meier paper since 1974. We are willing to bet that no reader can, without help from the Internet or a friend, guess a scientific paper that has a larger number of citations.

A good description of how the Kaplan-Meier test is carried out can be found in Chapter 12 of the British Medical Journal's on-line statistic book "Statistics at Square One."

The Kaplan-Meier test requires that we construct a life table for Oscar winners and the control group. We start by reminding our readers how Life Tables are constructed for the US population. The most recent US Life Tables can be found in CDC's National Vital Statistics Report Volume 58, Number 18 and are based on 1998 data. Life tables are given by sex and gender and also for the total US population. The following table is from the first 10 rows of the Life Table for the 1998 US population.

Year


Proportion
dying during
age interval


Number living
at beginning of
age interval


Life expectancy
at beginning of
age interval

x
q(x)
l(x)
e(x)
0-1
0.00721
100000
76.7
1-2
0.00055
99279
76.3
2-3
0.00036
99225
75.3
3-4
0.00026
99189
74.3
4-5
0.00021
99162
73.4
5-6
0.0002
99141
72.4
6-7
0.00019
99121
71.4
7-8
0.00018
99102
70.4
8-9
0.00017
99085
69.4
9-10
0.00015
99068
68.4

Table 1. From the 1998 US Population Life Table.

The first column indicates the first 10 age intervals.

The second column gives the proportion q(x) dying in each age interval, determined, as the number who died in this interval in 1998 divided by the US 1998 population at the midpoint of the age interval.

The third column starts with a cohort of 100,000 at birth and gives the number expected still to be alive at the beginning of each age interval. To compute these numbers we start with l(1) =100000 and then use the recursion relation  l(x+1) = l(x)(1- q(x)) for x > 1. (Note that 1-q(x) is the proportion of those alive at time x that survive at least one more year.) For example, l(2) = 100000(1- .00721) = 99279, l(3) = 99279(1-.00055) = 99,225 etc. The quantity l(x) can be interperted as the probability that a newborn child will live to year x. For any year t greater than or equal to x, the quantity l(t)/l(x) can be interpreted as the probability that a person who has lived to year x wil lives to year t.

To determine the life expectancy of a newborn baby we need only sum l(x) for all x. (Recall that for a discrete random variable X the expected value of X can be computed by the sum over all x of Prob(X >= x)). To find the life expectancy for a person who has reached age x we add the values of l(x)/l(t) for t greater than or equal to x. From the table we see that the life expectancy for a person at birth is 76.7 while for a person who has survived 9 years it is 69.4 making a total life expectancy of 79.4. Thus there is a 2.7 year bonus for having survived 9 years. You can view the entire Life Table here and check your own bonus. We have 10 year bonus for surviving so long but, alas, only a 10.7 year additional expected lifetime.

A survival curve is a plot of the probability l(x)/100000 of living x or more years as a function of age. Using the full life table we obtain the following survival curve for the US population.

Figure 1 Survival curve for US population 1998

For a discussion of the technical problems in producing and interpreting Life Tables see the article "A method for constructing complete annual U.S. life tables"  by R. N. Anderson.

We return now to the Oscar study. In studies like this and others where the Kaplan-Meier test are used, we have incomplete information about the length of time to the end effect-- death in the case of the Oscar study. Some of the Oscar winners will have died by the time the study is completed but others will not have died by this time. Still others may have been lost by the researchers after being followed for some time. For those who have not died we know only that they lived to a certain age and at this point we say that they have "left the study." The Kaplan-Meier procedure allows us to use this information along with the information, about those who have died, in making life tables.

Dr. Relemeier provided us with the data needed to carry out the Kaplan-Meier test. In Table 1 we show the first 10 entries in his data set for the members of the control group:

Number of years x lived
when died or left the study

0 means died in year x
1 means lost to the study in year x

56
0
79
1
38
1
71
1
69
0
78
0
48
0
52
0
82
0
61
1

Table 2: How the data is presented.

The first column gives the number of years that it is known the actor survived. For the first actor this was 56 years and the 0 in column 2 indicates that this actor died in his 56th year. The second actor survived 78 years and the 1 in column 2 indicates that this actor was lost to the study in his 79th year.

Recall that in the actual study there were 235 Oscar winners and 887 controls. To discuss how the Kaplan-Meier test works, using a manageable number of subjects, we chose a random sample of 30 Oscar winners and a random sample of 100 controls from the author's data set.

We first want to determine a survival curve for each of the two sample groups. Recall that the key information for determining a survival curve for the US population was the estimate q(x) of the probability that a person who has lived to the beginning of year x survives this year. We use the same quantity to construct the survival curve when we have incomplete information. This is done by constructing Table 2.

In column 2 of Table 2 we have listed, in increasing order, the years that the 30 Oscar winners died or were lost to the study.

In column 3 we put a 0 if the actor died and a 1 if the actor was lost to the study. Note that in some years there was more than one actor. For example there were three actors who either died or were lost to the study in their 54th year -- one died and two were lost to the study.

In column 4 we put the number n(x) of Oscar winners known to be alive at the beginning of year x.

In column 5 we put the number of Oscar winners d(x) who died in year x. Then (n(x)-d(x))/n(x) is the proportion q(x) of those alive at the beginning of year x who survived this year. These values appear in column 6.

Finally we use q(x) to estimate for the probability that an Oscar winner will live at least to the beginning of year x. As in the case of the tradition life table, l(0) = 1 and, for values greater than 0, l(x) is calculated by the recursion equation l(x) = l(x-1)*(1-q(x)). The values of l(x) appear in the last column.

Case The year x that an Oscar winner died or left the study A 0 means the winner died in year x and a 1 means the winner was lost to the study in year x The number n(x) of Oscar winners known to be alive at the beginning of year x The number d(x) of Oscar winners who died in year x The proportion q(x) of those life to the xth year who survived this year The proportion l(x) of Oscar winners who survived at least x years
0 1
1 27 1 30 0 1 1.000
2 37 1 29 0 1 1.000
3 38 1 28 0 1 1.000
4 45 1 27 0 1 1.000
5 50 1 26 0 1 1.000
6 51 1 25 0 1 1.000
7 54 1 24 1 23/24 0.958
8 54 1
9 54 0
10 57 1 21 1 20/21 0.913
11 57 0
12 61 0 19 2 17/19 0.817
13 61 0
14 63 1 17 0 1 0.817
15 65 0 16 1 15/16 0.766
16 69 1 15 0 1 0.766
17 73 1 14 0 1 0.766
18 73 1
19 74 1 12 0 0.766
20 75 1 11 0 0.766
21 77 0 10 1 8/10 0.612
22 77 0 0.612
23 78 0 8 1 7/8 0.536
24 81 0 7 1 6/7 0.459
25 82 1 6 0 0.459
26 84 0 5 1 4/5 0.367
27 85 0 4 1 3/4 0.276
28 92 1 3 0.276
29 93 0 2 1 1/2 0.138
30 96 1 1 1 1 0.138

Table 3 Determining the survival probabilities.

Plotting l(x) we obtain the following survival curve for the Oscar winners.

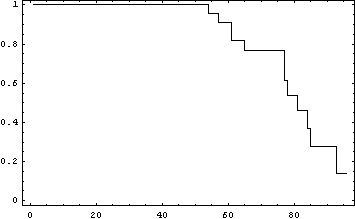
Figure 2 The Survival curve for the sample of Oscar winners

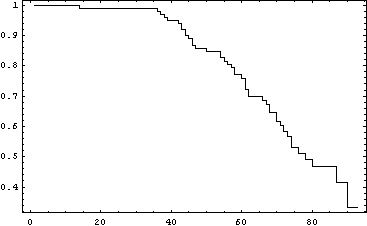
Making a similar table for the sample control group and plotting the survival curve we obtain the survival curve for this group:

Figure 3 The Survival curve for the sample control group

Putting the two together for comparison we obtain:

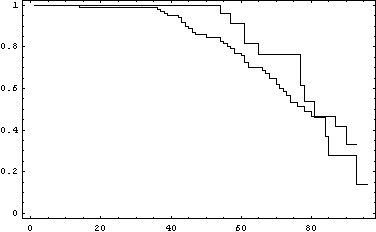
Figure 4 Survival curve for the sample of 30 Oscar winners and 100 controls

The upper curve is the survival curve for the winners and the lower curve is for the controls. These curves suggest that the winners do tend to live longer than the controls. We can get another indication of this by computing the expected lifetime for members of each group. As in the US population we simply summing l(t) over all years t. Doing this we find that the expected lifetime for an Oscar winner is 78.7 and for members of the control group it is 74.7 again indicating that the Oscar winners live longer on average than the controls.

We wrote a program for the above calculations. We then used this program to compute the survival curves for the original study with 235 Oscar winners and 887 controls. Here are the results:

Putting the two together for comparison we obtain:

    Figure 5 Survival curves for all 235 Oscar Winners and 887 controls

    Again the top curve is the survival curve for the Oscar winners and the bottom curve is for the control group. Using all the data we find that the expected lifetime for an Oscar winner is 79.7 and for the controls it is 75.8 which reflect the same difference we saw in our sample estimates of 78.7 and 74.7.

    We must now tackle the question of how the authors concluded that the approximately four years difference found in the study was significant, i.e., could not be accounted for by chance. For this, the authors used a test called the "log-rank test".

    We say an event happened in age year x if either at least one subject died or was lost to the study during this year.For each group and each age year we count the number still being followed at the beginning of the year and the number of deaths during this year. For example, in our sample we find that in the age year 61 we were still following 19 Oscar winners 2 of whom died in this year. For the control group we were still following 65 controls one of whom died this year. Thus there was a total of 84 still being followed at the beginning of age year 61 and a total of 3 deaths during this year. Now, under the hypothesis that there is no difference between Oscar winners and the controls, these 3 deaths should be randomly chosen from the 84 people still being followed. Thus we can imagine an urn with 84 balls, 19 marked O for Oscar winner and 65 marked C for controls. Then father death chooses three balls at random from this urn to determine the deaths. Then the number of the number of deaths chosen from the Oscar winners group has a hypergeometric distribution. The probability that any particular death is an Oscar Winner is 19/84 so the expected number of Oscar winners deaths in year 61 is 3*(19/84) =..679. The observed number o was 1. We also need to calculate the variance of the number of deaths among the Oscar winners. This is more complicated because the variance for the multinomial distribution is complicated.

    Assume that you have n balls in an urn, k are red and and n-k are black. Then if you draw m balls at random the expected number of red balls is

                                                                               e = m(k/n)
    and the variance is

                                                       v = ( m*(k/n)*(n-k)/n)*((n-m)/(n-1)).

    In our example the red balls are Oscar winners so the variance for the number of Oscar winners who died in the 61th year is

                                                      v = 5*(19/84)*(65/84)*(81/83)= .854

    Then to carry out the rank-order test we do the above calculations for each age year for a particular group. We chose the Oscar winners. Let O be the sum of the observed number of Oscar winners who died in each year, E the sum of the expected values over all years and V the sum of the variances over all years, Then the statistic

                                                        S = ((O-E))/sqrV

    will, by the Central Limit theorem, be approximately normal so S^2 will have approximately a chi-square distribution with 1 degree of freedom. Note that in summing the variances we are assuming that the observed numbers of Oscar winners who die in different years are independent. This is true because we are conditioning on knowing the number in each group that we are still watching and the total number of deaths for a given year. These determine the distribution of the number of Oscar winners who die in this year under our assumption that there is no difference between the two groups.

    Using our program to carry out these calculations for the data for this study we found S^2 = 9.1246. The probability of finding a chi-squared value greater than this is .0025 so this indicates a significant difference between the Oscar winners group and the control group.

    To check our program we carried out the calculations for the Kaplan-Meier procedure, as did the authors, using the SAS statistical program. SAS yielded the same survival curves as our program and for the significance tests SAS reported:

     

    Test Chi-Square Degrees of freedom Prob >
    Chi-Square
    Table 4. Significant tests produced by SAS

    Thus the log-rank test agreed with our calculation. SAS also provided two other tests that might have been used both of which would result in rejecting the hypothesis that there was no difference between the two groups. This ends our saga

                                             <<<========<<



    >>>>>=============>
    Copyright (c) 2001 Laurie Snell

    This work is freely redistributable under the terms of the GNU
    General Public License published by the Free Software Foundation.
    This work comes with ABSOLUTELY NO WARRANTY.

    !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !!!!!!!!!!!!!!!!

    CHANCE News 10.06

    May 21, 2001 to July 4, 2001

    !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!