Prepared by J. Laurie Snell, Bill Peterson, Jeanne Albert, and Charles Grinstead, with help from Fuxing Hou and Joan Snell.
We are now using a listserv to send out Chance News. You can sign on or off or change your address at this Chance listserv. This listserv is used only for mailing and not for comments on Chance News. We do appreciate comments and suggestions for new articles. Please send these to:
jlsnell@dartmouth.edu
The current and previous issues of Chance News and other materials for teaching a Chance course are available from the Chance web site.
Chance News is distributed under the GNU General Public License (so-called 'copyleft'). See the end of the newsletter for details.
It is evident that the primes are randomly distributed but, unfortunately we don't know what 'random means.'
R.C. Vaughan
Contents of Chance News 10.11
1. Forsooth.
2. A Ripley Forsooth.
3. Fifth grade students to see Harry Potter movie an average
of 100,050,593 more times.
4. Bamboozled by statistics.
5. Is a record warm November evidence of global warming?
6. Study suggests that Lou Gehrig's disease is associated with
service in the Gulf War.
7. What Stanley H. Kaplan taught us about the SAT.
8. Richardson's statistics of war.
9. Shotgun wedding magic.
10. The newspapers' recount suggests that the Supreme Court did
not determine the winner.
11. A statistical argument that the 17th Earl of Oxford authored
the works of Shakespeare.
12. Chance Magazine has a new editor.
13. Are there boy or girl streaks in families?
14. We return to Lewis Carroll's pillow problem.
In Chance News 10.10 Dan Rockmore wrote Chapter 1 of our story Chance in the Primes. This story is intended to help our readers understand Peter Sarnac's popular exposition of the Riemann Hypothesis. Astute readers have asked "where is the chance?" . In this Chapter we will give some examples of how chance is used in the study of primes. We hope this will provide some background for our next installment we will show the connections of random matrices to the Riemann Hypothesis.
Here is a table of the first 225 prime numbers
|
2
|
3
|
5
|
7
|
11
|
13
|
17
|
19
|
23
|
29
|
31
|
37
|
41
|
43
|
47
|
|
53
|
59
|
61
|
67
|
71
|
73
|
79
|
83
|
89
|
97
|
101
|
103
|
107
|
109
|
113
|
|
127
|
131
|
137
|
139
|
149
|
151
|
157
|
163
|
167
|
173
|
179
|
181
|
191
|
193
|
197
|
|
199
|
211
|
223
|
227
|
229
|
233
|
239
|
241
|
251
|
257
|
263
|
269
|
271
|
277
|
281
|
|
283
|
293
|
307
|
311
|
313
|
317
|
331
|
337
|
347
|
349
|
353
|
359
|
367
|
373
|
379
|
|
383
|
389
|
397
|
401
|
409
|
419
|
421
|
431
|
433
|
439
|
443
|
449
|
457
|
461
|
463
|
|
467
|
479
|
487
|
491
|
499
|
503
|
509
|
521
|
523
|
541
|
547
|
557
|
563
|
569
|
571
|
|
577
|
587
|
593
|
599
|
601
|
607
|
613
|
617
|
619
|
631
|
641
|
643
|
647
|
653
|
659
|
|
661
|
673
|
677
|
683
|
691
|
701
|
709
|
719
|
727
|
733
|
739
|
743
|
751
|
757
|
761
|
|
769
|
773
|
787
|
797
|
809
|
811
|
821
|
823
|
827
|
829
|
839
|
853
|
857
|
859
|
863
|
|
877
|
881
|
883
|
887
|
907
|
911
|
919
|
929
|
937
|
941
|
947
|
953
|
967
|
971
|
977
|
|
983
|
991
|
997
|
1009
|
1013
|
1019
|
1021
|
1031
|
1033
|
1039
|
1049
|
1051
|
1061
|
1063
|
1069
|
|
1087
|
1091
|
1093
|
1097
|
1103
|
1109
|
1117
|
1123
|
1129
|
1151
|
1153
|
1163
|
1171
|
1181
|
1187
|
|
1193
|
1201
|
1213
|
1217
|
1223
|
1229
|
1231
|
1237
|
1249
|
1259
|
1277
|
1279
|
1283
|
1289
|
1291
|
|
1297
|
1301
|
1303
|
1307
|
1319
|
1321
|
1327
|
1361
|
1367
|
1373
|
1381
|
1399
|
1409
|
1423
|
1427
|
In his lecture on the Prime Number Theorem Jeffrey Vaaler pointed out that it is hard to see any pattern in these numbers other than that they are odd numbers. This apparent randomness in the distribution of prime numbers has suggested to some that even though the primes are a deterministic sequence of numbers, we might learn about their distribution by assuming that they have some of the properties of a typical sequence from this chance process. An interesting example of this approach appeared in the 1936 paper of Harold Cramer "On the order of magnitude of the difference between consecutive prime numbers," Acta. Arithmetic, 2, 23-46. Of course, we know Cramer from his work in probability and statistics and in particular from his classic book "Mathematical Methods of Statistics" still in print. However, his thesis, and early work, was in prime number theory.
In an interesting article
"Harald Cramer and the distribution of prime numbers" Scandanavian
Actuarial J. 1 (1995), 12-28.
Andrew Granville writes:
Gauss in a letter to Encke, on Christmas eve 1947, writes (liberally translated)
As a boy I considered the problem of how many primes there are up to a given point. From my computations, I determined that the density of primes around n, is about about 1/log(n).
While 1/log(n) is not a probability density since its sum on n is infinite, it has proved useful to think of 1/log(n) as the probability that the nth number is prime. For example, we shall see later that modern incryption methods require identifying prime numbers with about 200 digits. If we chose 200 digitis at random then we would expect to have to test log(10^200) or about 461 200 digit numbers to find a 200 digit prime number. We tried it an on the first try got the following prime number
920818223736917811496594651773959966773461318011455519502153076699683673743109571148 407290872646563495260839513768092873538312702985117800736511260477249905 09562469510870262814853787658789749590614753.
Cramer considered the following very simple chance process to investigate questions about the prime numbers. He imagined a sequence of urns U(n) for n = 1,2,... He puts black and white balls in the urns in such a way that if you choose an urn at random from the kth urn it will be white with probability 1/log(k). Then you choose 1 ball from each urn and n is a Cramer random prime if the nth ball you drew from the urn was white. In his paper Granville describes a number of results that Cramer proved for his pseuo-primes that led to a better understanding of the true primes. We shall illustrate this in terms of a result that held for random primes which led to an interesting conjecture that has not yet been settled for the true primes.
In his earlier research Cramer had been interested in the gaps that occur between prime numbers We define the nth gap as the difference p(n+1)- p(n) where p(n) is the nth prime. These gaps can be arbitrarly large. To see this one has only to note that n! - j is divisible by j for 2 <= j <= n so there must be a gap of at least n-1. We say that a gap is a record gap if, as we go through the sequence of primes, this gap is larger than any previous gap.For example, for the first 10 primes 3,5,7,9,11,13,17,19,23,29 the gaps are 2,2,2,2,2,2,4,2,4,6 so the record gaps are 2,4,6. The record gap 6 beginns at 23 and ends at 29.
For pseudo primes Cramer proved, using the Borel-Cantelli lemma that, with probability 1, the ratio of the nth record gap to the square of the logarithm of prime that stared the gap tends to 1. That is the record gaps are asymptoically the log(p)^2 where p is the prime where the gap starts.
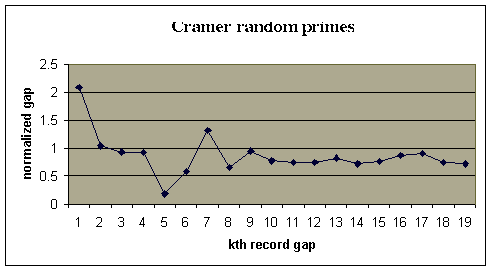
We have simulated Cramer's chance process to obtain a sequence of a hundred-million pseudo-random primes. In this sequence there were 19 record gaps. Here is a graph of the ratios of these gaps normalized by dividing by the square of the beginning prime.

r convergence to 1.
Let's compare this with a graph of the normlized record gaps for
real prime numbers. Record gaps are provide here
by Thomas Nicely. From his records we see that there are 63 record gaps known
with the largest record gap equal to 1132. This gap starts at the prime 1693182318746371.
The log(1693182318746371)^2 = 1229.58 so this record gap normalize is 1132/1229.58
= .92 which is close to the limiting ratio of 1 given by the Cramer conjecture.
Here is a graph of the 63 normalized record gaps.
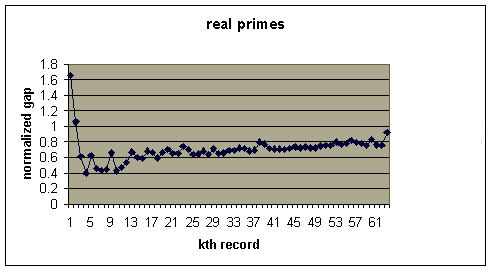
This picture does appear to support the Cramer conjecture.
We have looked at large gaps between primes but what about small gaps. Except for the first two prime numbers (2,3) the smallest gap that could occur is 2. When this occurs we say we have twin primes. One of the biggest unsolved problems in mathematics is: are there infinitley many twin primes? Let's see if this is true for the Cramer process. Let E(n) be the event that n and n + 2 are random primes. Then P(E(n)) = 1/log(n)log(n+2). The events E(n) are independent and the sum of their probabilities diverges. Thus by the Borel-Cantelli lemma with probability one infinitely many of the events E(n) will occur and we will have infinitely many twin random primes. We might wonder why such a simple proof does not work for the real primes. To see why we introduce another technique introduced by Eratosthenes of Cyrene (275-194 BC) and now called the Eratoshenes Sieve.
The Eratoshenes Sieve is a technique to determine pi(n), the number of primes less than or equal to n. There are several applets to demonstrate how it works. We illustrate how it works for n = 200 using an applet that you can find here.
We start with a table of the integers from 1 to 200.
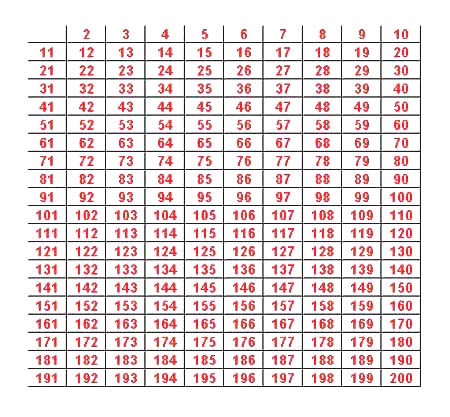
We then proceed to "sieve out" all the numbers divisible the first prime number 2.
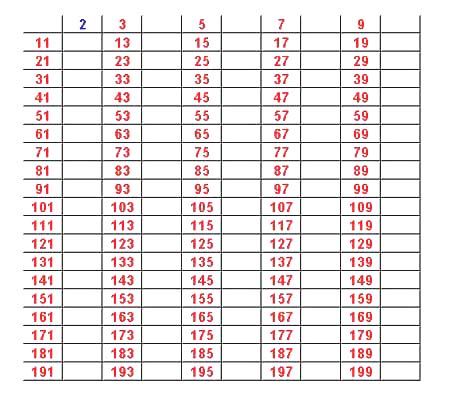
Next we sieve out from the red numbers those divisible by 3 obtaining:
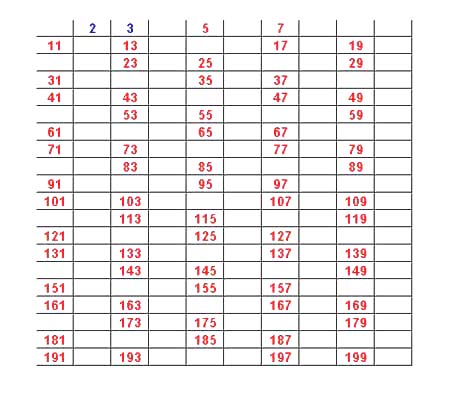
Now we sieve out the red numbers divisible by 5:

Finally we sieve out the red numbers divisible by 7 leaving us with only primes.

Here is a probability derivation of the prime number theorem suggested by this sieving process. Assume that we choose a number at random from 1 to n. Then the probability that it is divisible by k is approximately 1/k and that it is not divisible by k is 1- 1/k. Thus the probability that X is prime is the probability that it is not divisible by any prime not greater than the square roos of n. Assuming that the events of being divisible by two different primes are independent we can write the probability that X is prime as:
(1-1/2)(1-1/3)(1-1/5) ... (1-1/p)
where p is the largest prime not greater than the square root of n.
But Mertens showed that this over all primes no greater than n is asymptotically
e^-gamma/log(n)
where gamma is Euler's constant. series. Thus, by Merten's theorem,
the product over all primes no greater than the square root of n would be asymptotically
e^-gamma/log(sqr(n)) = 2e^-gamma/log(n) = 1.2292.../log(n).
and so we would have proved that the probability that X is prime is asymptotically 1.2992../log(n) contridicting the prime number theorem which states that this probability is 1/sqr(n).
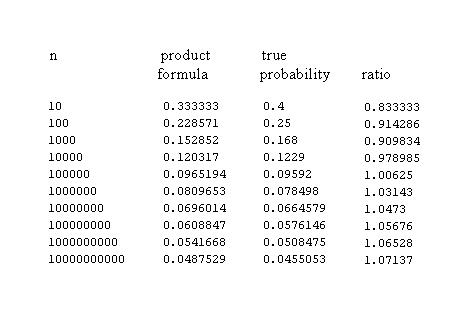
But the probability that X is prime is also the proportion of numbers no greater than n that are prime. By the prime number theorem we know that this is asymptotically 1/log(n). What is wrong with our argument? There are two things wrong. Consider our example of n = 200. The number divisible by 2 is 100 so the probability that our random number is not divisible by 2 is 1/2. However, the number divisible by 3 is floor(200/3) = 66 so the proportion divisible of 3 is 66/200 = .33. Thus the probability that X is not divisible by 3 is .66 rather than 2/3 as in the product. The second problem is that these events are not independent so we cannot simply multiply the probabilities. Here is are the probabilities that X is prime computed by our product compared with the true probability obtained by counting the number of prime numbers no greater than n.
The Eratoshenes Sieve suggested to David Hawkins a chance process that would generate random primes that might have properties closer to the prime numbers than did Cramer's random primes. He defines his process by a probability sieve. Start with the integers beginning with 2:
2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,...
Now throw out each number with probability 1/2. This might give us
2,4,5,7,10,11,13,14,17,18,19,23,...
Then start with the second number, in this case 4, and throw out each larger number in the sequence with probability 1/4 leaving for example,
2,4,10,14,17,18,23,...
Then start with the third number 10 and throw out each larger number in the sequence with probability 1/10. Continue in this way to obtain a sequence of random primes.
Of course, it is easy to simulate random primes. Here are the primes less than 1000 in one such simulation:
2 4 6 12 16 19 26 28 30 34 37 41 43 44 52 57 60 61 68 70 75 81 83 88 89 91 94 100 103 105 107 111 117 130 131 134 135 137 146 152 157 163 172 173 174 175 176 193 198 205 208 211 215 218 222 223 228 241 256 257 263 269 271 287 290 291 298 302 313 322 324 352 358 377 380 382 384 389 398 412 420 429 431 433 435 444 451 474 485 492 495 497 500 529 546 562 564 568 571 583 599 602 603 610 625 626 629 640 644 661 663 669 681 693 699 706 709 719 733 738 742 752 767 782 792 802 810 814 839 840 861 869 894 905 907 910 911 912 919 923 924 927 938 940 962 966 970 981 982
Hawkins and others proved a number of theorems similar to theorems for prime numbers. For these theorems we think of a random sequence of numbers that have been selected by Hawkins method as the random primes. His method determines a probability measure on the space of all sequences and we say that a theorem related to a specific sequence or random primes is true with probability 1 if it holds for almost all sequences using this probability measure.
For example,Wunderlich showed that with probability one a sequence of random primes satisfies the prime number theorem. That is, the number of random primes less than n is asymptotically n/log(n). In our simulation there are 150 random primes less than 1000. The prime number theorem would predict 1000/log(1000) = 144.77 which is closer than the result for real primes but, of course, both estimates are meant to be for large n.
Wunderlich proved that with probability one, the product of (1-p) for p a random prime less than n is asymptocially 1/log n. This is the probablistic analog is Merten's theorem except for real primes this product was asymptotically e^-gamma/log n. Thus this is a case where the Hawkins' random primes do not give the same result as the true primes.
One of the biggest unsolved problems in prime number theory is to prove or disprove that there are invinately many "twin primes". A twin prime is a pair of successive odd numbers both of which are prime.For example, the first four twin primes are (3,5), (5,7), (11,13) and (17,19). The largest known twin prime is a 32,220 digit number 318032361*2^107001+ or - one found by Underbakke and Carmody.
Since even numbers can be prime with random primes a natural "twin prime" theorem for random primes would be that there are infinitely many twin random primes of the form k, k+1. Wunderlich showed that for Hawkins' random primes this is true with probability one. He also showed that with probability one the number of twin primes less than n is asymptotically n/(log n)^2.
For true primes we can get a heuristic estimate for twin(n) by assuming that the occurrance of a twin prime at n and n+2 are independent. Then using the prime number theorem the probability that for odd n (n,n+2) is a twin prime 1/log(n)*log(n+2). Thus we would expect the number of twin primes less than n to be asymptotically n/(log n)^2 . Hardy and Wright gave this argument but then gave an improved estimate suggesting that it is asymptotically Li2(x) defined by
Li2(x) = c*Integral[1/log^2(x), {x, 2, n}]
where c is a constant equal to 1.3203...This estimate is remakably good. From this web site we find an interesting discussion of twin primes and the following table comparing the Hardy Wright estimate with the true numbers of twin primes for values of n for which the number of twin primes is known todate.
|
n
|
Twin primes < n
|
Hardy Wright estimate
|
Relative error
|
| 10 | 2 | 5 | 150 |
| 100 | 8 | 14 | 75 |
| 1000 | 35 | 46 | 31.43 |
| 10000 | 205 | 214 | 4.39 |
| 100000 | 1124 | 1249 | 11.12 |
| 1000000 | 8169 | 8248 | .97 |
| 10000000 | 58980 | 58754 | -.38 |
| 100000000 | 440312 | 440368 | .013 |
| 1000000000 | 3424506 | 3425308 | .023 |
| 10000000000 | 27412679 | 27411417 | -.0046 |
| 100000000000 | 224376048 | 224368865 | -.0032 |
| 1000000000000 | 1870585220 | 1870559867 | -.0013 |
| 10000000000000 | 15834664872 | 15834598305 | -.00042 |
| 100000000000000 | 135780321665 | 135780264894 | -.000042 |
| 1000000000000000 | 1177209242304 | 1177208491861 | -.0000064 |
| 5000000000000000 | 5357875276068 | 5357873955333 | -.0000025 |
Of course it is natural to ask if one can use probability methods to prove that the Riemann Hypothesis is true with probability one or at least to give reasons why the this hypothesis should be true. In our next chapter we will describe a current method that deals with the zero's of the zeta function itself. Earlier methods have concentrated on trying to show that statements equivalent to the Riemann Hypothesis are true. Most of these have involved the mobius function so we will describe this approach.
Recall that the zeta function for s > 0 the zeta function has the form
z(s) = 1 + 1/2^s + 1/3^s + 1/4^s +...
and the product formulat for z(s) is
z(s) = (1/1-2^-s)(1/1-3^s)(1/1-5^s)...
where the product is over all primes.The reciprical of the zeta function, d(s) for s > 0 is
1/z(s) = 1/mu(1) + 1/mu(2) + 1/mu(3) +...
where mu(n) is the mobius function has the value 0 if n if is divisibible by a square and otherwise equals 1 if the number of prime factors is even and -1 if this number is odd. To verify this one has only to form the product of these two series and see that everything cancels out except 1.
Here are the values of mu(n) for n = 1 to 20
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| mu(n) | 1 | -1 | -1 | 0 | -1 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | -1 | 1 | 1 | 0 | -1 | 0 | -1 | 0 |
Let's count the number of integers k less than n for which the the mu(k) is -1 or 1. This will be the case if k is not divisible by any squares of prime numbers-- that is that it is square-free.. The fraction of such numbers will be the probability that a randomly chosen integer betwee 1 and n is square-free. Using the same probability argument we used in calculating the probability that a random number from 1 to n is prime we find the the probability
Prob(square-free) =(1-1/2^2)(1-1/3^2)(1/1/5^2)(1-1/7^2)...
where the product is over all primes whose squares are less than the square root of n. If we take the reciprical of this probability we see that we have a partial product in the product formula for 1/zeta(2). This suggests that the proportion of square free integers should approach 1/zeta(2) = 6/pi^2. This method of computing the probability that a random number from 1 to n is square free is similar to our product to calculate the probability that that a random number from 1 to n is prime that did not work. However, then we were dealing with a probability that tends to 0 and trying to obtain an asymptotic result. Here was expect the probability to tend to a limit. But to be sure it works here is a caculations for large values of n compared to the limiting value 6/pi^2.

We see that the product formula does give the correct answer in the long run but we have to go out pretty far to get it. Of course we can also compute the exact value to see how this compares our prediction for the limiting value.
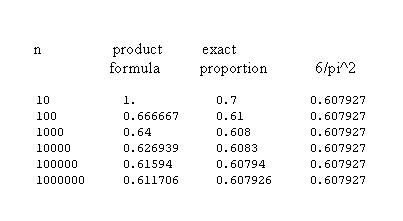
From this we see that the exact computation for the proportion of square free numbers approaches the limiting value faster than the product formual.
In Chance News 10.10 Dan Rockmore wrote Chapter 1 of our story Chance in the Primes. This story is intended to help our readers understand Peter Sarnak's popular exposition of the Riemann Hypothesis. Astute readers have asked "where is the chance?" . In this Chapter we will give some examples of how chance is used in the study of primes. We hope this will provide some background for our next installment we will show the connections of random matrices to the Riemann Hypothesis.
Our first example of chance and primes relates to the problem of sending secure messages on the internet. Obviously, internet commerce depends upon being able to send information such as your credit card securely.
The problem of encoding messages has a long history and you can read about this here.
We shall discuss this topic in terms of a very simple problem. Alice wants to send Bob his grade in such a way that if someone reads Bob's e-mail they will not know her grade. She gives grades A,B,C,D,E, or F and wants to code them before sending them to her students. A simple method, that goes back to the way Caesar communicated with his troops, is to encode each letter as a different letter. For example, encode each letter as the letter 3 positions further along in the alphabet, starting at A again when F is reached. If Bob got an A she would send him a D, if he got a B she would send him an E, etc. The amount of the "shift" (in this case it is 3) acts as a "key" to the code and the way to assign the letters using this key is called the "codebook". Thus Alice's key is 3 and her "codebook" is
A B C D E F D E F A B C
When Bob gets the message he will decode it by his codebook
D E F A B C A B C D E F
Thus if Alice sends Bob an E he will decode it as a B.
Henry is intercepting the student's mail and wants to decode the grades. In other words he wants to know what Alice has used for a key. Well, if Henry intercepts the grades of everyone (or even a reasonable fraction of the class) then Henry could almost surely figure out the shift by looking at the distribution of the grades that he intercepted, and then shifting it back to make it look more reasonable (presumably, in a bog class the grade distribution should be bell-curve like with a median around C, assuming no grade inflation!). Having done this he would probably recognize Alice's scheme of just shifting the grades.
The problem of keeping the enemy from deducing the key by intercepting messages, has, for centuries, haunted those who used codes. The story of the breaking of the German enigma code used in World War II is a fascinating story which you can read about here. (WHERE?)
The recognition that it would be easy for internet messages to be intercepted led to develop coding methods that would make it difficult to decode the message sent even if the encoded messages were intercepted. An example of this is the RSA code named after it's authors Ronald Rivest, Adi Shamir, and Leonard Adleman. We will explain this method for coding messages.
We will illustrate the RSA method using our example of Alice sending a grade to Bob. The RSA method is a bit complicated but fortunately Cary Sullivan and Rummy Makmur have provided here an applet to show how it works. We shall follow this applet in our explanation.
We start by choosing two prime numbers p and q and compute their product n = p*q. To keep things simple, the applet allows you to pick only small numbers for p and q but in the actual application of the RSA method p and q are chosen to be large primes with about 200 digits so that n has about 400 digits. The reason for this is that we are going to want the whole world to know n but not p and q. This will work because there is no known method to factor 400 digits number in a reasonable amount of time. Also, our RSA encryption method changes a message into a number m and will only work if m < n so unless n is large we are limited in the number of different messages we can send at one time.
Responding to the applet we choose the two primes p= 7 and q = 11. Then n = p*q = 77. Next we use the Euler function Phi(n) whose value is the number of numbers less than or equal to x that are relatively prime to n. (Two numbers are relatively prime if they have no common factors). When n is the product of two prime numbers p,q, Phi(n) = (p-1)*(q-1) since there are q multiples of p, and p multiples of q that are less than or equal to pq, and in each of these sets of multiples the number pq is included, so there are exactly p + q -1 multiples of either p or q less than or equal to pq, or pq - p - q +1 = (p-1)(q-1) numbers relatively prime to pq. Thus,
Phi(n) = Phi(7*11) = 6*10= 60.
Next, the applet finds a number e which is relatively prime to Phi(n). It chooses the smallest such number which is 7. The number e is called the "exponential key." In mod n arithmetic, x has a multiplicative inverse y if xy =1 mod n. (Recall that x mod n is the remainder when n is divided by x). To have such an inverse, x and n must be relatively prime. Since e and Phi(n) are relatively prime, e has an inverse mod(Phi(n)) which we denote by d. The applet finds that d = 43. To check this we note that ed = 7*43 = 301 = 1 mod 60. The numbers n and e are called "public keys" and can be made publicly available. The number d is called the "private key" and available only to Bob to decode the message from Alice.
Bob's grade was a B. Alice uses numbers to represent the grades with A = 1, B = 2, etc. so she wants to send the message m = 2.
Alice encrypts her message m as c = m^e mod n. Thus c = 2^27 mod 77 = 51.
Then since d is the mod n inverse of e, ed = 1 mod n. Thus Bob can determine m by computing c^d mod n. This works because
c^d mod n = (m^e)^d mod n = m^(ed) mod n = m mod n = m. Here we have used that m < n.
Well, we still have not mentioned chance. Chance comes in when we try to choose the 200 digits prime numbers p and q. Standard tests for primality cannot handle numbers this big. However, it turns out there is a simple method of determining numbers with about 200 digits which have an extremely high probability of being random. The method for doing is suggested by a theorem of Fremat
Fermat's (Little) Theorem: If p is a prime and if a is any integer, then a^p = a mod p
A number p for which a^p = a (mod p) is called a "probable-prime". By Fermat's theorem every prime is a pseudo-prime. However not every probable-prime is prime. But if we choose a probable-prime at random it is very likely to be a prime. .Just how likely has been determined by Su Hee Kim and Carl Pomerance. For they showed, for example, that if you pick a random 200 digit probable-prime the probability that n is not prime is less than 00000000000000000000000000385. You can find more precisely what random means here.
It is natural to ask how hard it is to test if a 200 digit number x is a probable-prime
is prime. Suppose you are using a base 2. Then we have to see if 2^(x-1) = 1
mod x. Fortunately it is practical to to raise 2 to such a high power by writing
it a a product of smaller powers of 2. This is called the method of repeated
squaring.