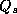 be the sensitive question and
be the sensitive question and 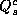 be its complement. For example
be its complement. For example
THE PROBLEM: How can we get accurate answers to a sensitive question which respondents might be reluctant to answer truthfully?
EXAMPLES: ``Have you ever used illegal drugs?"
``Do you favor a constitutional admendment that would outlaw most abortions?"
``Have you had more than one sexual partner in the past 6 months?"
``Have you ever driven a motor vehicle while intoxicated?"
METHOD #1: Warner (1965)
Let 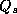 be the sensitive question and
be the sensitive question and 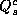 be its complement. For example
be its complement. For example
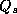 = ``Have you ever used a sick day leave when you weren't really sick?" YES N0
= ``Have you ever used a sick day leave when you weren't really sick?" YES N0
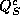 = ``Have you never used a sick day leave when you weren't really sick?" YES N0
= ``Have you never used a sick day leave when you weren't really sick?" YES N0
With some (known) probability 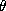 a subject gets
a subject gets 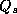 , otherwise (with probability
1 -
, otherwise (with probability
1 - 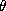 ) he or she will answer
) he or she will answer 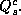
KEY POINT: The respondent determines which question he or she answers using some probability device which is under his or her control.
Example: Have the respondent roll a die. If the result is { 1, 2, 3, or 4 } answer
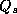 , if the die is {5 or 6} answer question
, if the die is {5 or 6} answer question 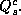 Since only the respondent knows
which question he or she is answering, there should be no stigma attached to
a YES or N0 response.
Since only the respondent knows
which question he or she is answering, there should be no stigma attached to
a YES or N0 response.
BUT, can we still estimate the proportion who would say YES to the sensitive question?
Let 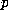 = proportion in the population for which the true response to
= proportion in the population for which the true response to 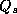 is YES.
So
is YES.
So  is the chance of getting a YES response to
is the chance of getting a YES response to 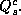 Given the Warner
randomized response scheme, the proportion of YES responses should be
given by
Given the Warner
randomized response scheme, the proportion of YES responses should be
given by
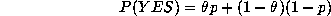
We solve easily for p to give
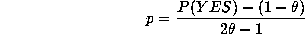
If the number of YES responses in a sample of size  is
is 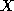 , we estimate p with
, we estimate p with
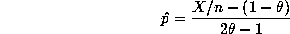
Question: What happens when 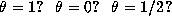
METHOD #2: The Innocuous Question
Replace 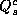 with an innocuous question,
with an innocuous question, 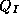 , which has a known probability of
yielding a YES response.
, which has a known probability of
yielding a YES response.
Example:
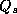 = ``Flip a coin. Have you ever shoplifted?" YES N0
= ``Flip a coin. Have you ever shoplifted?" YES N0
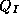 = ``Flip a coin. Did you get a head?" YES N0
= ``Flip a coin. Did you get a head?" YES N0
Again, the respondent does 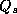 with probability
with probability 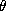 and has a
and has a  chance to
answer
chance to
answer 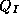 . If the known probability of a YES to
. If the known probability of a YES to 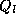 is
is  , we find that overall
, we find that overall
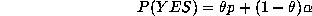
Solve for p to give
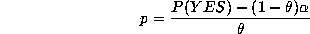
and the estimator based on  responses of YES in a sample of size
responses of YES in a sample of size  becomes
becomes
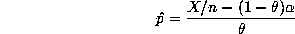
**********
Question: Which method is more efficient?
To compare them we need to examine the variances of each sample proportion estimate.
Note: If we could ask the question directly, we know that 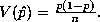
For Warner's Method #1:
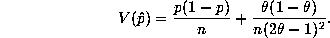
For the Innocuous Question Method #2:
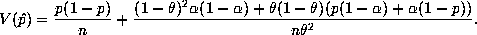
If 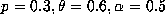 we can calculate
we can calculate
Method #1 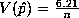
Method #2 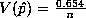
 Innoccuous Question method is almost ten times more efficient than Warner's method.
Innoccuous Question method is almost ten times more efficient than Warner's method.
Some References for Randomized Response:
This document was generated using the LaTeX2HTML translator Version 0.6.4 (Tues Aug 30 1994) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 RResponse.tex.
The translation was initiated by J. Laurie Snell on Mon Apr 17 16:32:56 CDT 1995