SCI199Y: November 14, 1995

Required for next week

Reading

"Does Exposure to Second-Hand Smoke Increase Lung Cancer Risk?", A.J. Gross and "What Evidence is Needed to Link Lung Cancer and Second-Hand Smoke?", H.E. Rockette, Chance 6 (4), 11-18.

Your task

Come prepared to discuss these articles, and to ask questions about the parts you didn't understand.

Notes on short project 4

Short project 4 hasn't been assigned yet, but it will require submission of a proposal for your final essay. My idea for this essay is that it will give an in-depth discussion of one of the topics we've come across in class. That could mean reviewing one or more books, summarizing a series of articles on a topic, following up on an article of interest,

Reading List on DNA fingerprinting

• Berry, D.A. (1990) DNA Fingerprinting: What does it prove? Chance 3 (3), 15-25.
• Cohen, J.E. (1990) DNA Fingerprinting: What (really) are the odds? Chance 3 (3), 26-32.
• National Research Council (NRC) (1992). DNA typing: Statistical basis for interpretation. In DNA Technology in Forensic Science 74-96. National Academy Press, Washington DC. (This is available on the WWW: the URL is http://www.geom.umn.edu/docs/snell/chance/teaching_aids/DNAtyping/).
• Roeder, K. (1994) DNA fingerprinting: a review of the controversy. (with discussion) Statistical Science 9, 222-278.

Some more applications of Bayes' theorem

To spousal abuse and murder

This is taken from the article in Chance that was handed out on October 31, attached to the Paulos article. Although they computed the odds ratio version, I find it easier to work with the ordinary version that I gave in last week's handout. In the formula at the top of p.3, replace "G" by "current or former mate murdered the victim" and "DNA match" by "a history of known abuse". To save space, I'll use "M" and "A" for these two cases. (If you hate notation, write out the formula in long-hand.)

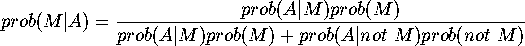
The article uses the following estimates:

My Hewlett-Packard gives the result on the left hand side as 0.8032; very close to 80%. If

is bumped up to 3/4, then I get 0.8595.

Recall that defense attorney Dershowitz referred to a probability of 1 in 1000 (the risk that a women in an abusive relationship has of being murdered each year). Where does this probability appear in the calculation above?

Random screening for HIV-prevalence

In any kind of screening for disease, the probability that we're interested in is

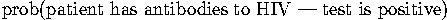
. Using Bayes' theorem again, we'll need the following pieces:

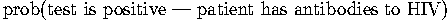
and

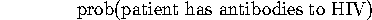
.We'll also need

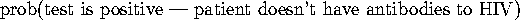
: this is also called the ``false-positive" rate of the test.

I got the following figures from the Chance News WWW page(URL: http://www.geom.umn.edu/docs/snell/chance/course/topics/aids.html) which includes the text of a New York Times editorial piece. The editorial took the figures from an article in the New England Journal of Medicine. The US Army does routine testing of recruits, and has a very careful testing procedure, with an estimated false positive rate of only 1 in 20,000. However, in the general population, the incidence of HIV is also rare: estimated to be 1 in 10,000. Assuming that the army's test misses no true positives, we get

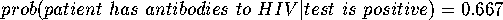
or about 2/3. That leaves a 1 in 3 chance that the patient does not have antibodies to HIV, after testing positive.

If the false positive rate is increased from 1 in 20,000 to 1 in 10,000, there is a 1 in 2 chance that the patient does not have antibodies to HIV, after testing positive. If the false positive rate is as large as 1 in 1,000, which it may well be expected to be if widespread screening were instituted, the same formula gives

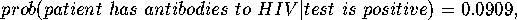
i.e. there is about a 90% chance that a randomly chosen patient testing positive does NOT have antibodies to HIV. For every 10 people testing positive, 9 of them will NOT have HIV.

What's driving this calculation is the small incidence of HIV antibodies in the general population (the 1 in 10,000 above). Screening in high risk groups would give much different numbers, because this probability would be much larger.

Technical note to follow

In the ``hot hand'' articles, there are several technical terms used: null hypothesis, alternative hypothesis, significance level, power. These are all related to a particular type of statistical inference called hypothesis testing, or sometimes significance testing. More on this next week.

In the Globe and Mail this week

• ``Switch prevents rampaging cells'' November 10, A7 Toronto research found that a deficiency in CTLA-4 leads to symptoms of autoimmune diseases in laboratory mice. The discovery is expected to lead to more information about the treatment of immune diseases. The full report appears in this week's Science.
• ``Hope rises for vaccine to prevent AIDS infection'' November 10, A7 Also taken from an article in this week's Science. At the last world AIDS conference, though, there seemed to be general agreement that a vaccine for AIDS was nowhere in sight.
• ``From monster home to white elephant'' November 10, A7 A report released by Statscan on November 9 projects increasing demand for small homes and decreasing demand for large homes, over the next 20 years.
• ``U.S. swimmer's lax penalty raises ire'' November 13, D5 A young (age 14) U.S. swimmer who tested positive for steroids was given 2 years probation; a penalty much milder than usually taken by national sports organizations. This reminded me about a recent article in Applied Statistics.
• ``Eateries live hand-to-mouth'' November 13, B6. The graphic caught my eye, but the story that might be of more interest is that this is the first of a series of articles examining industry sectors using data provided by Dun & Bradstreet, Canada.
• ``U of T again dominates in ranking'' November 13, A6. The dreaded MacLeans report is out again. How do they come up with these numbers anyway?
• ``Entrepreneurs now outnumber civil servants'' November 13, A6. This reports data from the Labor Force Survey of Statscan. So what is the labour force survey, and how does one get hold of a copy?

• Wringing The Bell Curve: a cautionary tale about the relationships among race, genes and IQ.
• A paradox in the ranking of figure skaters.
• Small cars, big cars: what is the safety difference?
• Racetrack betting: do bettors understand the odds?
• Baseball: pitching no-hitters.
• Baseball's earned run average: what kind of an average is it?
• The baby boom generation and how they grew.
• Resizing triathlons for fairness
• Can TQM improve athletic performance?
• The best NFL field goal kickers: are they lucky or good?
• What happened to HIV transmission among drug injectors in New Haven?
• Answering questions about baseball using statistics.
• The state of state election polls.
• How much more efficiently can humans run than swim?
• Statistical evidence of cheating on multiple choice tests.
• Should pregnant women move? Linking risks for birth defects with proximity to toxic waste sites.
• Scientific inferences and environmental health problems.

About this document ...

This document was generated using the LaTeX2HTML translator Version 0.6.4 (Tues Aug 30 1994) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -split 0 lec9.tex.

The translation was initiated by Marie K. Snell on Thu Nov 16 14:54:23 CST 1995