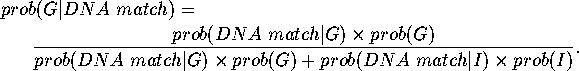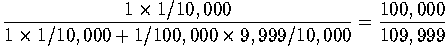No Title

SCI199Y: November 7, 1995

Required for next week

Reading: "The Cold Facts About the `Hot Hand' in Basketball", A. Tversky and T. Gilovich, and "Basketball, Baseball and the Null Hypothesis", R. Hooke, Chance 2 (1), 16-21 and (4), 35-37.
Your task: Come prepared to discuss these articles, and to ask questions about the parts you didn't understand.

Notes on short project 3

The second question should have said "... newspaper or magazine article about a poll...'' [italics mine]: I didn't mean any misleading article!
The things that I'll look for are (a) an answer to the questions asked, (b) some discussion vis-a-vis the poll guidelines (c) clear and convincing writing

The last may seem a bit vague, and it is hard to pin it down completely, but as a general guideline, try to make each sentence count. Check for errors of grammar and/or spelling. When you read your discussion, can you see what the main points are? Is it to the point, or does it ramble? Does it have a clear start and end?

Paulos on O.J. Simpson

You will recall that John Allen Paulos' OpEd piece on the O.J. Simpson trial (handed out last week) included a calculation of a probability that was 1/4000. (This was computed as 1/8 x 1/500; rough estimates of the probability of the Mr. Simpson having the same shoe size as the perpetrator times the probability of Mr. Simpson sustaining a cut on his left side on the night of the murder.)

This 1/4000 probability is referred to in the third paragraph (top of p.2) as ``a very strong indicator of guilt''. However, in the fifth paragraph he seems to refer to the 1/4000 probability as ``the probability of an innocent person's having all this evidence arrayed against him''. This latter description is the correct interpretation; as Kathy pointed out, in the language of conditional probability it would be described as the

probability of an individual having this evidence arrayed against him,
given that he was innocent.

As noted in the handouts for this week, the

probability of an individual being innocent,
given this evidence arrayed against him

is not only ``not quite the same thing'' (Paulos' words), it can be a very different thing. Paulos has, in my opinion, confused these two probabilities by his reference to guilt in the second paragraph.

Conditional probability and Bayes' theorem

The probability of an event is the long run frequency of its occurrence. For example, if you flip a fair coin, the probability of heads is 1/2. If you toss a fair die, the probability of a 3 is 1/6. If you deal one card from a deck, the probability that it's an Ace is 1/13 = 4/52.
Two events are independent if the occurrence of one does not make the occurrence of the other more or less probable. If two events are independent, the probability of both of them occurring can be calculated by multiplying. For example, the probability of 2 heads in 2 flips of a fair coin is 1/2 x 1/2 = 1/4. The probability of double 3's in a roll of two dice is 1/6 x 1/6 = 1/36.
Events are often dependent. A nice example from BN: a neighbourhood that has a lot of Mercedes probably does not have a lot of homeless people. When events are dependent, the probability of one event, say A, given that the other event, say B, has occurred, is now the frequency of occurences of A among situations where B has occurred. For example, the probability that the sum of 2 dice is 10 or more, given that one dice shows 6, is 1/2. (The possible throws are (6,1),(6,2)(6,3)(6,4)(6,5)(6,6): half of them give a sum of 10 or more.)
The probability of A given B can be very different from the probability of B given A. An example given in BN is the following: the probability that one speaks Spanish, given that one is a citizen of Spain, is about 95%. On the other hand, the probability that one is a citizen of Spain, given that one speaks Spanish, is only about 10%.
In DNA testing as used in the courts, the results of the test give
probability(defendant's DNA profile matches the profile of the sample from the scene of the crime, given that the defendant is innocent)
usually reported briefly as ``prob(DNA match | innocent)''. This is usually a small, even tiny, probability. What the jury has to think about is
probability(defendant is innocent, given a DNA match)
and this can be much larger.
The key to computing one conditional probability from the other one is Bayes theorem. Since we're using it in the context of DNA testing, I'll give the formula in terms of that:
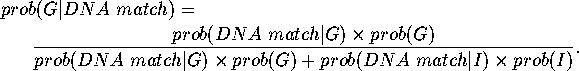
The probability of a DNA match given the defendant is guilty is usually taken to be 1. The probability of a DNA match given the defendant is innocent is the usually very small probability mentioned above.
Here's a hypothetical calculation taken from The prosecutor. Suppose that the DNA testing lab reports that a match has been obtained, and that the probability of a match is 1/100,000. Further, suppose the jury believes that the defendant is one of 10,000 individuals who could have been at the scene of the crime and that the non-DNA evidence does not distinguish between these individuals. In this case it would be appropriate for the jury to assign the values pr(guilty)=1/10,000 and pr(innocent)=9,999/10,000. Then on the basis of all the evidence, the probability that the defendant is guilty can be computed as
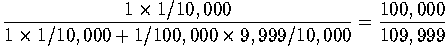
or about 91%. Stated more positively, there is a 9% chance that the defendant is innocent. (Not 1 chance in 100,000.)
I found the following references helpful.
[BN]
Beyond Numeracy. John Allen Paulos, 1991. Vintage Paperback. (entry on probability)
[The prosecutor]
The prosecutor's fallacy and DNA evidence. D.J. Balding and P. Donnelly. in The Criminal Law Review, October, 1994.

Numeracy. John Allen Paulos, 1988. Vintage Paperback.

The book Statistics by Freedman et al. (see last week's handout) has a nice discussion of People vs. Collins, one of the first examples in the courts to confuse the two conditional probabilities discussed here.

In the Globe and Mail this week

``Campaign hoopla belies calm pattern of opinion polls'' (October 31, A4). Gives a table showing all the polls conducted from Sept. 9 through Oct. 27. Subheadline says ``...rise and fall of Yes and No support rarely varied more than plus or minus 3 per cent''. We knew that.
``How Quebec voted'' (November 1). A data map that drives home the fact that data maps visually confuse population with area.
``Ontario set to test all Grade 3 pupils'' (November 2, A16). Recommendations from the Education Quality and Accountability Office will be implemented this year and next. They include testing of all students in Grades 3 and 11, and ``random sample testing of students in Grade 6 and 9, which would provide a snapshot of the system''.
``Breast cancer gene may be pivotal'' (November 4, A5), ``Study confirms existence of gay gene in men'' (October 31, A12), ``Gene's link to heart and brain poses dilemma'' (November 1, A8). Just in case you thought genetics wasn't important. The last article is taken from the New York Times, and is by Gina Kolata, who often reports on science issues.
``Students' drug use takes big jump'' (November 3) ``Drug use has increased dramatically among Canadian high-school students.'' A study by the Addiction Research Foundation indicates twice as many students report having smoked marijuana in 1995, as in 1993. A table is given that provides information on consumption of other drugs. The ARF report is probably publicly available. The questionnaire was administered by the Institute for Social Research at York University. The article also mentions that the ARF has been surveying drug use in Ontario for 18 years.
``Trials set for pill to perk up desire'', November 3, A1 & A8. Couldn't resist.

About this document ...

The command line arguments were:
latex2html -split 0 lec8.tex.

The translation was initiated by Marie K. Snell on Thu Nov 16 15:10:23 CST 1995

laurie.snell@chance.dartmouth.edu