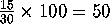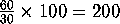SCI199Y: October 3, 1995

Percentages and percentiles

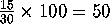1. Percentages are ratios of two numbers, multiplied up by 100. 15 is fifty percent of 30. (). 60 is two hundred percent of 30. ().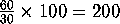
2. Percentiles are `percentage-cut-points' for a list of numbers. Ten percent of any list is smaller than the tenth percentile. Fifty percent of any list is smaller than the fiftieth percentile. And so on. The 50th percentile is usually called the median. The 25th and 75th percentiles are sometimes called the upper and lower quartile. Here is a list of 20 numbers: 68 60 63 98 20 51 30 4 33 49 53 92 89 21 99 93 58 83 69 97. Here they are in order from smallest to largest: 4 20 21 30 33 49 51 53 58 60 63 68 69 83 89 92 93 97 98 99. The median is 61.5, and the upper and lower quartiles are 41 and 90.5. (This uses an averaging argument: 41 is halfway between 33 and 49, 61.5 is halfway between 60 and 63, and 90.5 is halfway between 89 and 92.)

In the news this week...

• "Tough employment picture for highschoolers'': G & M, Oct.2 (A6) Employment rate and average earnings for males with high school diplomas have dropped since 1979. [with accompanying graphic]
• "Statscan releases data on senior couples": G & M, Sept. 29 (A6) Reliance on pensions rising, investment income declining. [with accompanying graphic]
• "Poll shows No side pulling ahead": G & M, Sept. 30 (A1). On p. B3, same day, "Dollar surges in wake of poll" (although it was a different poll).

Required for next week

• Anything that didn't get done for this week.
• Read Chapters 7 ,8 and 9 in VDQI. Come to class prepared to note the parts you didn't follow, and the parts you found particularly interesting.
• Come to class prepared to indicate some preference for themes to be discussed in the course (refer to handout for September 12).
• Find an article in a journal that includes a statistical graphic. Bring a copy of the graphic, and be prepared to provide a brief description of the article and the full source reference. Scientific journals that have articles for the `educated layperson' include: Scientific American, American Scientist, Science, Nature, Mathematical Scientist, Chance, The Sciences. Other journals of possible interest include J. Amer. Medical Assoc., New England J. Medicine, Lancet, Psychology Today, The Economist, History Today, ...

Project 1 continued

The graphic that I chose is taken from the Annual Report on International Statistics, Volume 2, 1995. This report is published by the International Statistical Institute, Voorburg, The Netherlands and provides an overview of recent activities of international statistical associations. The article in which this graph appears is ``The internet and statistical educators'' by T. Arnold, (pp. 9-10). It shows the amount of information transferred over the internet from November 1992 to January 1995, categorized by type of interaction. In addition to the generally increasing trend in use of the internet, it is striking that the use of the world wide web has been increasing much more quickly: as of January 1995 more bytes were transferred using the web than any other method of internet access except ftp-data transfers.

The graphic is rather poorly drawn and reproduced, so the central message is obscured. The circles plotted for each data point are an example of what Tufte calls redundant data ink, and are visually distracting. The frame around the graph is ``chartjunk''. The source of the data should be indicated in the legend of the figure, where it would not distract from the message of the data. The five categories of internet usage could be coded with different line types (or different grey scales) to give a more pleasing and clearer picture. A conversion of the scale of the 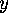-axis to bytes would be more informative.

The Monty Hall problem continued

The correct solution, assuming that Monty always opens a door that does not have the prize (and this is a crucial assumption), is to switch. You have 2/3 chance of winning if you switch, and 1/3 chance of winning if you do not switch. Here is how the solution is laid out in Engel and Venetoulias (1991):

Reference Engel, E. and Venetoulias, A. (1991) Monty Hall's probability puzzle. Chance 4, 6-9.

About this document ...

This document was generated using the LaTeX2HTML translator Version 0.6.4 (Tues Aug 30 1994) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -split 0 lec4.tex.

The translation was initiated by Marie K. Snell on Thu Nov 16 15:03:41 CST 1995