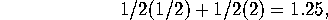
Here is the infamous Monte Hall problem, as it appeared in the Parade Magazine of 9 September 1990:
Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say number 1, and the host, who knows what's behind the doors, opens another door, say number 3, which has a goat. He then says to you, ``Do you want to pick door number 2?'' Is it to your advantage to switch your choice?
What assumptions does your answer depend on?
Here is another paradox having to do with switching from one choice to another.
Two envelopes each contain an IOU for a specified amount of gold. One envelope is given to Ali and the other to Baba and they are told that the IOU in one envelope is worth twice as much as the other. However, neither knows who has the larger prize. Before anyone has opened their envelope, Ali is asked if she would like to trade her envelope with Baba. She reasons as follows. With 50 percent probability Baba's envelope contains half as much as mine and with 50 percent probability it contains twice as much. Hence, its expected value is
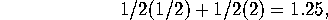
which is 25 percent greater than what I already have and so yes, it would be good to switch. Of course, Baba is presented with the same opportunity and reasons in the same way to conclude that he too would like to switch. So they switch and each thinks that his/her net worth just went up by 25 percent. Of course, since neither has yet opened any envelope, this process can be repeated and so again they switch. Now they are back with their original envelopes and yet they think that their fortune has increased 25 percent twice. They could continue this process ad infinitum and watch their expected worth zoom off to infinity.
John Finn has suggested starting with a simpler problem. Suppose Ali and Baba know that I am going to give them either an envelope with 5$ or one with 10$ and I am going to toss a coin to decide which to give to Ali, and then give the other to Baba.
Here is another paradox closely related to the previous one. Ali and Baba are again given two envelopes with an IOU for a specified amount of gold in each envelope. This time they know nothing about the amounts other than that they are non-negative numbers. After opening her envelope, Ali is offered the chance to switch her envelope with that of Baba. Can Ali find a strategy for deciding whether to switch which will make her chance of getting the envelope with the larger of the two numbers greater than one half? At first blush, this would appear to be impossible.
But consider the following strategy: Ali does an auxiliary experiment of choosing a number
by some chance device that makes all non-negative numbers possible. For example, choose
to be the number of tosses of a fair coin until the first head turns up. If the IOU given Ali is greater than
she keeps this envelope, if it is less than
she switches to the other envelope.
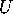is between the two numbers in the envelopes then Ali will always
be correct with the strategy we have suggested.