!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
CHANCE News 4.14
(1 October 1995 to 20 October 1995)
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Prepared by J. Laurie Snell, with help from William Peterson,
Fuxing Hou, Ma.Katrina.Munoz.Dy, and Joan Snell, as part of the
CHANCE Course Project supported by the National Science
Foundation.
Please send comments and suggestions for articles to
jlsnell@dartmouth.edu.
Back issues of Chance News and other materials for teaching a
CHANCE course are available from the Chance Web Data Base
http://www.geom.umn.edu/locate/chance.
======================================================
In God we trust, all others must use data.
Edward Deming
======================================================
Contents
1. A challenging real world problem.
2. M&M homepage.
3. More on "Alphabetism".
4. Seeking the truth in a vast gray area.
5. Paulos comments on the Simpson trial.
6. Did Simpson jury distort reasonable doubt?
7. Keno is as popular in delis as in bar.
8. A pox on your average.
9. Attitudes and anxieties about race.
10. Unconventional wisdom.
11. CBS tests its pilots at Las Vegas lab.
12. A comparison of polls.
13. Ask Marilyn: good hands attract.
14. How many were in the Washington march?
15. Cigarette ads most powerful influence on youths.
16. Small acquittal rate in wife killings.
17. The crime scene.
18. Study links excess vitamin A and birth defects.
=============================================================
A CHALLENGE: Shunhui Zhu plays basketball once a week with 9 others who want to choose
two teams of five at random from their 10 players. They have been using the strategy
of asking each person to toss a coin hoping to get five heads and five tails. If
so, these are the teams. If not they try again. (They actually use the fist and hand
method instead of tossing a coin). Last week, Pete suggested it would be more efficient
if he did not toss his coin. If there was a five-four split for the other nine he
would join the four group. If not, they could repeat this procedure. Was this a more
efficient method? What method should they use if they want to minimize the expected
number of coins tossed? Ben Tilly can achieve expected number of tosses 7 3/64 but
his method is not very practical. His best practical solution is around 13.5. Can you
improve on either of these?
=============================================================
Note: Those who do the famous M&M experiment might like to go on the tour provided
on the M&M homepage
<<<========<<
>>>>>==========>>
The reference for the article "Alphabetism" in the last Chance News should have been
"Royal Statistical Society Newsletter", Sept. 1995 Letters: Ernest Rudd, York.
In this note, Rudd mentioned his article: "The effect of alphabetical order of author
listing on the careers of scientists", Social Studies of Science", 7, 268-269 (1977).
This article reported Rudd's attempt to see if joint articles typically have the
authors listed in alphabetical order (they do) and if being listed first helped scientists
get ahead (apparently not).
Rudd looked at chemistry departments in UK universities during the year 1974 and found
no significant difference in the distribution of first letter for last name of professors
compared to all faculty. We compared the 2116 members of the National Academy of Science and the 3695 with Dartmouth students in residence Fall 1994. We obtained
the following spectacular similar distributions:
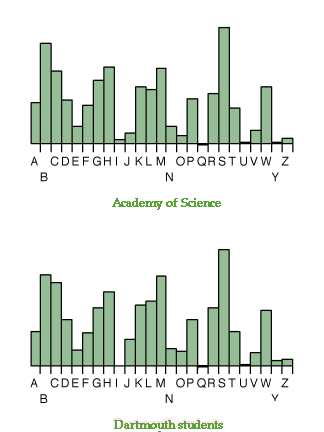
<<<========<<
>>>>>==========>>
In scientific studies, seeking the truth in a vast gray area.
New York Times, 11 October 1995, C1
Lena Williams
This article reports on a one day meeting of epidemiologists and journalists in Boston
to try to find solutions to the media confusing the public with contradictory recommendations
on medical issues. There was plenty of blame to go around. Scientists tend to overstate their findings to get attention or grants or both. Journalists add
to the problem by focusing on the most controversial or titillating aspect of medical
research. Finally, the public is too anxious to find quick fixes.
The recent study linking moderate weight gain in middle-aged women to an increased
risk of death was held up as an example of the problems. The issues in this study
were complicated and many of the accounts did not give enough details to indicate
how the findings differed depending on race, eating patterns, etc. In addition the report
that its author serves as an adviser to two companies that make diet pills created
doubts about the study,
The scientists reviewed some of the reasons that their findings may not be accurate:
biases, inaccurate reporting by subjects, and other methodological problems. They
agreed that they use too much jargon and present the journalist with an almost impossible task of learning about the results and explaining them in a non-technical way with
only a few days study. They recommended that the articles be released to journalists
weeks in advance rather than days in advance.
DISCUSSION QUESTIONS:
The Dartmouth Chance class discussed this article with a science writer and asked
her the following questions among others:
(1) Why does the media feel compelled to report so many results on issues like the
value of drinking a glass of wine a day when the studies are often contradictory?
(2) Are science writers acting ethically when they report preliminary findings and
know the public will over-react to their reports?
(3) Which specific newspapers or magazines give the most accurate reports of medical
results? How do T.V., magazines, and newspapers compare in accuracy?
(4) What article or articles have you most enjoyed writing? Ans. Ones that allow
me to get to know and feel, at least vicariously, what it is like to be leading a
life completely different from my own.
<<<========<<
>>>>>==========>>
Mathematics he wrote.
Philadelphia Inquirer, 15 Oct. C7
John Allen Paulos
This is an OpEd piece discussing some of the misunderstandings about probability and
statistics brought to light by the Simpson trial.
Paulos starts by discussing the statement by Dershowitz (lawyer on the Simpson defense
team) that, since fewer than 1 in a 1000 women who are abused by their mates go on
to be killed by them, the spousal abuse in the Simpsons' marriage was irrelevant
to the case. (See Chance News 4.10)
He next reminds the reader what independence means and points out that, if you have
several pieces of evidence that could be reasonably assumed independent, you can
get a pretty small number for the probability that an innocent person would fit these
pieces of evidence. He says that retreating to the fact that you really want the probability
that the person is innocent, given the evidence, not the probability of the evidence,
given innocence, does not help much. Paulos suggests that these considerations led the defense to choose to emphasize the conspiracy and cover up approach.
<<<========<<
>>>>>==========>>
Did Simpson jury distort reasonable doubt?
New York Times, 6 October 1995, A30
Steven de Savlo: Letter to the editor.
The writer, a lawyer, writes that, in his opinion, the Simpson case reflected a common
misunderstanding of reasonable doubt. He says "It appears that some people, including
the Simpson jurors, have distorted this legal standard into a nearly insuperable
barrier to conviction, one that requires that every single piece of evidence be proved
beyond a reasonable doubt."
As evidence of this he reminds us of the many statements made during and after the
trial pointing out "a thread of evidence in the quilt of guilt woven by the prosecution
that, for one reason or the other, proved to be less than conclusive.
DISCUSSION QUESTION:
It is sometimes argued that jurors should encouraged to think about starting with
an initial probability of guilt and modify this as the evidence unfolds (i.e. think
Bayes). Is this a good idea? Is it realistic?
<<<========<<
>>>>>==========>>
Keno is as popular in delis as in bars.
New York Times, 17 Oct. 1995, B6
Ian Fisher
New York has a new game called Quick Draw, a form of Keno. It is outpacing projections
for how much money in would bring in by almost 20 percent. The game was intended
primarily for bars and restaurants, but some of the top selling outlets are convenience stores and other stores where alcohol is not sold. The article discusses some of
the concerns about where the game is being played and how it is being played. The
fact that you can play a new game every five minutes suggests to some it may be additive.
None of the articles discussing this game gave the actual details of how it is played.
We consulted our New York sources and found that it is played as follows: You specify
a set of numbers chosen from the first 80 integers. You can have from 1 to 10 numbers in your set. The computer then picks 20 numbers at random from the integers
from 1 to 80. You can bet 1,2,3,4,5, or 10 dollars. You are paid off according to
how many numbers are in both your set and the set chosen by the computer. Here
are the payoffs per dollar bet. The row number represents the number of elements in the set
you choose, and the column the number in your set that match numbers chosen by the
computer..
0 1 2 3 4 5 6 7 8 9 10
1 2
2 10
3 2 23
4 1 5 55
5 2 20 300
6 1 6 55 1000
7 1 2 20 100 5000
8 2 6 75 550 10000
9 2 5 20 125 3000 30000
10 5 2 10 45 300 5000 100000
DISCUSSION QUESTIONS:
(1) When you play, you get a card to submit your choices. In addition to the above
table the card tell you the probability that you will win something for each choice
for number of elements in set you choose. Is this what a gambler would want to know?
(The card also gives you a phone number to call if you feel you might be a compulsive
gambler.)
(2) What is your expected payoff if you choose one number? If you choose 3 numbers?
(3) Donald Trump and others tried to stop this game on the grounds that it was not
a lottery as defined by the State Constitution and thus not exempt from New York's
general prohibition against gambling. A judge ruled that "the game contained all
the essential features of a lottery: i.e. consideration for chances, represented by numbers
drawn at random, and a prize for the winning number of numbers. A lottery agent
inserts the player's picks into a computer terminal--the player does not. Nor does
the machine eject anything of value as would a slot machine--only a bet slip used by the
player to compare the numbers to those drawn and displayed on the video screen."
Does this ruling make sense to you?
(4) Do you think this is a good way for New York to solve its monetary problems?
<<<========<<
>>>>>==========>>
Roger Johnson suggested the next article.
A pox on your average.
Star Tribune, 6 Oct. 1995, 7C
Rachel Blout
A report at the annual conference of the American Psychological Association suggested
that the Sports Illustrated jinx does exist. Researchers studied the batting averages
of 58 major league players before and after they appeared on the cover of the magazine between 1955 and 1995. They found that these players averages declined about 50
points. They studied at-bats, hits, RBI, total bases, and other data.
They found the most marked decline appears two to three weeks after the cover appearance
and speculated that the decline might be caused by the player trying too hard to
live up to the cover appearance. In addition, they suggested the player might suffer
"a natural letdown" after achieving such a milestone.
DISCUSSION QUESTIONS:
(1) If you look at players when their batting averages reach new highs what do you
think these players averages will do in the next two weeks on average?
<<<========<<
>>>>>==========>>
Reality Check: Attitudes and Anxieties about Race.
The Washington Post, 8 October 1995, A26
Malcolm Gladwell
Even though African-Americans make up only 12% of the U.S. population, most Americans
think they constitute a greater proportion. In fact, whites estimated an average
23.8%.
The survey, conducted by The Washington Post, the Henry J. Kaiser Family Foundation,
and Harvard University, involved 1,970 randomly selected adults.
The survey found that a person's estimate of the black population is drawn from the
individual's personal experience with blacks and whether that person lives in an
area with a large black population. The study found that whites who come in contact
with many blacks at home or at work tend to make higher estimates of the total black population
than those who live in more racially homogeneous areas. Richard Nadeau, a University
of Montreal political scientist, says: "People who see minorities around them reach the conclusion that these people form an important proportion of the total population.
It's a classic case of people exaggerating their own experience."
The Post also reports that people's ideas about the proportion of minorities depend
heavily on their own attitudes about race. A random sampling of those in the poll
who held the most exaggerated ideas about the size of the black population revealed
that they also had a persistent fear of and animosity toward African Americans.
To explain this, the "group conflict" theory of racism has been proposed by psychologists
and political scientists. According to this theory, whites practice racism in response
to a perception of political or social threat from blacks, and the greater the perceived threat the greater the response. For instance, Chicago (40% black) has
greater housing segregation than Tucson (5% black).
<<<========<<
>>>>>==========>>
Unconventional wisdom.
The Washington Post, 8 October 1995, C5
Richard Morin
Four studies reveal some interesting new facts and statistics about Americans.
(1) A Nation of Stooges.
A recent survey by The Luntz Research Companies in Arlington, Virginia, found that
55% of Americans could not name a single justice of the U.S. Supreme Court, but 59%
could name the three Stooges. 6% could name four, and 2% could name all five. (Over
the course of their movie lives, there were five Stooges: Moe, Larry and Curly -- the
core Stooges -- and also Shemp and Curly Joe.)
(2) The Politics of Safety.
Harvard economist Steven Levitt analyzed crime and police staffing data from the 59
largest cities in the country whose mayor is directly elected. He found that there
is less crime in big cities during and immediately after mayoral and gubernatorial
election years than in non-election years.
Levitt found that mayors and governors boost the number of police officers to appear
tough on crime. A 1% increase in the number of sworn officers resulted in a 1% decline
in violent crime. For every officer added, there is a decrease of 4 to 5 crimes.
(3) They Write the Songs.
Psychologist M.L. Corbin Sicoli of Cabrini College analyzed biographical data on all
45 women who wrote at least two Top 50 songs between 1960 and 1990 and found the
following statistics about their personal lives:
(a) 48% had lost a parent as a child
(b) 64% experienced problems in establishing and
maintaining intimate relations with men
(c) 68% experienced mental disorders (substance abuse,
anxiety, depression)
(d) 72% left home before they were 19 yrs. old
(e) 78% didn't graduate college
(4) The Heavy Cost of Crime.
Economist Levitt of Harvard updated the work of Vanderbilt law professor Mark Cohen
that estimates the real cost of crime to society. He totaled the haul in burglaries
and robberies but also included "quality of life" costs (based on compensatory damages
awarded to crime victims in civil cases). What he found is that one murder, on average
costs society $2.7 million, and one assault case costs $10,200.
<<<========<<
>>>>>==========>>
Beth Chance writes:
Recently I participated in a CBS screening
survey (you get to watch a TV show and push
little controls for parts you like and parts
you don't like, heaven for me). When I asked
if I could steal some of their questionnaires
for my Intro Stats class they were less than
forthcoming. They did mention a Wall Street
Journal article that gave an in-depth overview
of their methods.
Here it is.
CBS tests out its pilots at Las Vegas lab.
Wall Street Journal, 23 May 1995, B1
Elizabeth Jensen
This article states that: "CBS figures that with 30 million visitors a year, a fairly
representative sample of the American TV audience troops through Las Vegas."
Therefore CBS has developed a "state of the art" laboratory to test reactions of visitors
to potential new series. The visitors watch a pilot of the series and, when they
see something they like, they push a green button on a hand held control. When the
show annoys them, they push a red button. A computer turns the push-button data into
a "vidigraph," a second-by-second graph of viewer reactions. This allows producers,
watching the graphic's peaks and valleys to pinpoint which characters are popular
and which jokes fall flat. Additional information is obtained from questionnaires.
The peak of the pilot season is mid-May and they have only a couple of weeks to test
three dozen new series candidates before the fall prime-time schedule is set. During
this period, CBS persuades as many as 900 visitors a day to visit the test center
on the second floor of Harrah's.
The article states that the process may not identify hits but is good at picking out
failures. A CBS executive is quoted as saying that: "No show has gotten a low score
and gone on to succeed. Only 10% of the time does it do better in the lab than on
the air.
DISCUSSION QUESTIONS:
(1) Harrah's estimates that 30,000 people a day pass in front of the casino each day.
Their median age is about 45, with slightly more women than men and an average household
income of about $45,000. Would you think the sample is representative of the national TV audience?
(2) The article states that some people doze off while watching the pilots. Their
votes are not counted. Should they be?
(3) NBC tests its shows on cable systems in several cities supplemented by focus-group
interviews. Those recruited give their opinion by telephone interviews. Which of
the two systems do you think would be the most effective.
<<<========<<
>>>>>==========>>
A comparison of polls.
Here are comments from Susan Lee about some articles that occurred earlier this year
but whose message is still timely.
I found great examples of polls from spring of this year. Three different newspapers
(The New York Times, The Los Angeles Times, and USA Today) published polls on Gingrich
right around the same time.
Buried in the innards of the LA Times (p. A16) on 3/30/95, they ran an article entitled,
"Gingrich Receives Mixed Reviews in Poll". About a week later (4/6/95), on the front
pages of the New York Times it proclaimed in large letters, "GOP Gets Mixed Reviews From Public Wary on Taxes." Further in the article, in smaller letters, it says
"Gingrich elicits unfavorable responses in a new opinion poll". The very next day
(4/7/95) on the front pages of USA Today, they proclaimed in letters almost an inch
tall, "Poll: 60% Give credit to Gingrich". Later in the article they cite statistics and
proclaim in large print: "Most say Gingrich King of the Hill," and "More like Gingrich
than dislike him".
What is a person to believe? Is Gingrich the "King of the Hill"? Or does he receive
unfavorable responses? A closer look at the USA Today poll reveals a flaw in their
reasoning. They asked people to rank on a scale of -5 to 5 how much they like or
dislike Gingrich, with -5 being extreme dislike, and 5 being extreme like. USA Today
then simply added up the number of people who gave a number between 1 and 5 (which
was 50 %). They also added up the number of people who gave a number between -5
and -1 (which was 44%). Then they concluded that more people like Gingrich than dislike him
because there were more people in the 1 to 5 category.
But this is clearly wrong. If they had simply asked, "Do you like or dislike Gingrich?"
the results would be quite different. And in fact, the New York Times poll asked
people, "Do you view Gingrich favorably or unfavorably?" and (as one might expect) their results were quite different. Indeed, one would expect that people who gave
a number between -4 and -5 in the USA Today poll would definitely say "unfavorable".
Likewise, the people who gave a number between 4 and 5 in the USA Today poll would
definitely say "favorable." But what about the large number of people in the middle
range, between -3 and 3?
If you add the percentage of people who answered between -3 and -5 in the USA Today
poll, that number is 30%. In the New York Times poll 29 % answered "Unfavorable".
If you add the percentage of people who answered between 4 and 5 in the USA Today
poll, that number is 17%. In the NYT poll, 16% answered "Favorable." I like this example
very much. It shows that the people who like Gingrich like him but not overwhelmingly
so. By contrast, the people who dislike Gingrich dislike him rather vehemently.
And this is a good example of how the wording of questions change the results of the
poll.
Reading the LA Times and the NY Times articles provide many other examples of how
subtle changes of wording affects the outcome polls. For example, in the LA Times
article, they report that 44% of the respondents said they approve of "Gingrich's
handling of his job as speaker". 37% disapproved. In the NY Times article, 39% of the respondents
said they approve of "the way Gingrich is doing his job". 34% disapproved. Both
polls polled about 1000 people. These differences are significant.
<<<========<<
>>>>>==========>>
Ask Marilyn.
Parade Magazine, 15 October 1995, p 13.
Marilyn vos Savant
A reader writes:
I've heard that when playing cards, when you're
dealt a pair, it increases the odds that your
opponent is dealt a pair, too. Is this true?
If so, how?"
Marilyn says it's true, and illustrates with a counting argument, assuming that you
and your opponent are each dealt 2-card hands. A pair in any of the 13 denominations
can be obtained in C(4,2) = 6 ways, by choosing a pair of suits. Marilyn demonstrates this by explicitly listing the combinations. Now, if you hold a pair you've eliminated
5 of your opponent's opportunities for pairs, since there remains only 1 way for
her to get a pair in the same denomination as you (there remain 6 options for any
other denomination). On the other hand, if you don't hold a pair, you reduce to C(3,2)
= 3 the number of ways she could get a pair in either of the two denominations you
hold. This is a total loss of 6 opportunities, which is one more than the 5 she
loses when you hold a pair. So her chances for a pair are indeed better when you hold a pair!
For more on problems like this, see S. Gudder, "Do good hands attract?" Mathematics
Magazine 54(1), 1991, pp. 13-16.
DISCUSSION QUESTION:
(1) Does Marilyn's argument extend directly to 5-card hands?
(2) Show that in poker a Royal Flush attracts a Royal Flush.
<<<========<<
>>>>>==========>>
BU analysis says Washington march may have drawn 1.1 million.
The Boston Globe, 20 October 1995, p 11.
Thomas C. Palmer, Jr.
Boston University's Center for Remote Sensing has analyzed computer enhancements of
photographs taken at Louis Farrakhan's Million Man March on Washington. Their estimate
for the number of participants is 870,000, with a margin of error of 25%. The upper end of this range is the 1.1 million cited in the headline. In any case, these figures
exceed the earlier US Park Service estimate of 400,000. BU's estimates were made
from still photos, which are said to be of better quality than the videotapes used
by the Park Service. Rev. Farrakhan has promised to challenge the Park Service in court.
He claims the actual number was 1.5-2 million.
Park Service figures are typically lower than those given by event organizers. Apparently
tired of all the criticism, the Park Service said it may give up doing the estimates.
While the article does not say whether BU is interested in the job, it does note that the Remote Sensing Center is usually involved in scientific studies concerning
the population of cities or number of trees in a forest. Director Farouk
el-Baz is a former NASA employee whose previous assignments include studying the lunar
surface and counting sand dunes for Operation Desert Storm.
DISCUSSION QUESTION:
(1) Does it surprise you that organizers are usually displeased with Park Service
estimates?
(2) How would you estimate the size of a crowd?
<<<========<<
>>>>>==========>>
Study finds cigarette ads most powerful influence on youths.
Boston Globe 18 October 1995, p 10
Dolores King
Results of a new survey, appearing in the "Journal of the National Cancer Institute",
suggest that cigarette advertising has more influence on whether adolescents start
smoking than does having friends or family members who smoke. The study surveyed
more than 3500 adolescents aged 12-17 who had never smoked, and followed them up several
years later. Those who were identified as most susceptible to marketing--because
they could name a favorite ad or owned a tobacco company's T-shirt--were almost four
times as likely to start smoking than youngsters who were not swayed by the campaigns.
A related study, to appear in the "Journal Health Psychology", links tobacco advertising
campaigns conducted between 1980 and 1977 to subsequent increases in youth smoking.
DISCUSSION QUESTION:
(1) The data reported do not compare the effects of advertising with the effects
of peer pressure. How do you think "susceptibility" to peer pressure was measured?
(2) A Tobacco Institute spokesman said that research by the Surgeon general and others
has shown peer pressure to be the main reason adolescents smoke. How could you control
for the effect of peer pressure in measuring the effects of advertising? What problems can you foresee?
<<<========<<
>>>>>==========>>
Study of wife-killing trials shows a small acquittal rate.
New York Times, 14 Oct. 1995, Sec 1 p. 7
Julia Campbell
This article begins by remarking that "only 2 percent of the men charged with killing
their wives are acquitted at trial, according to a study of spousal murder cases
resolved in 1988 in 75 of the nation's largest urban counties." It is an
interesting exercise to read the following more detailed statistics given in this
article and try to get the big picture.
The study looked at 540 cases in 1988 involving 318 men and 222 women accused of killing
their spouses. It found that women were less likely than men to be convicted, with
70 percent of the women being found guilty compared with 87 percent of the men. Race of the accused or the victim or the jury members did not appear to play a role in
the conviction rate.
The article goes on to say that of the male defendants in the study, 46 percent pleaded
guilty, 41 percent were convicted at trial, 2 percent were acquitted at trial and
11 percent were not prosecuted. Of the 91 men who were tried by a jury, all were
convicted.
Of the women arrested, 39 percent pleaded guilty, 31 percent
were convicted at trial, 14 percent were acquitted at trial and the 16 percent were
not prosecuted.
DISCUSSION QUESTIONS:
(1) Do you think the 2% figure emphasized is misleading?
(2) Is it reasonable to say that 70 percent of the women were found guilty when,
in fact, 39% pleaded guilty and 31 percent were convicted?
(3) What highlights of this study would you have chosen to emphasize if you were
writing the article?
<<<========<<
>>>>>==========>>
The crime scene.
The Boston Globe Magazine, 10 September 1995, p11.
Katherine Whittemore
Last summer there were numerous news stories on declining crime rates. For example,
New York City murders were down by 1/3 and robberies by 1/5. This article challenges
pronouncements by law enforcement officials that the declines are attributable to
stepped-up police work and other get-tough policies. It argues that most of the decline
can be explained by demographic factors.
Expert opinion on this issue is offered by James Alan Fox, dean of the College of
Criminal Justice at Northeastern University. Fox believes crime rates directly reflect
the population of the most crime-disposed age group: the 14-34 year-olds. The relatively low numbers presently in that age group offers a simple explanation for the crime
statistics. He cites the years 1980-85 as another period where that age group was
low percentage of the population. Crime rates during that period declined 23%, but
those figures did not receive much press attention. This time around, with more public
attention focused on crime, there is more reason for officials to try to take credit
for the decline.
Fox makes it clear that he is not arguing that police work has no effect but says
that demography is the most predictable factor: "We may not know how many more police
officers we'll have in 2005, or how many prison cells, or what the streets will look
like, but we will know how many teens will be out there--23% more than there are today."
He thinks that we are in for a big disappointment if we think we've won the war
on crime, and warns against cutting social programs that help potentially crime-disposed groups.
DISCUSSION QUESTION:
1. Should we expect a 23% increase (a popular figure in this article!) in the crime
rate? How would one go about predicting the size of the effect?
<<<========<<
>>>>>==========>>
Study Links Excess Vitamin A and Birth Defects.
New York Times, 07 October 1995, Page 1 and 7
Jane E. Brody
A new study conducted by Dr. Kenneth J. Rothman and his colleagues at Boston University
Medical School has found that babies, of women who consumed more than 10,000 international
units of vitamin A daily from supplements or food or both were more likely to be born with malformations of the head, heart, brain, and spinal cord.
The study followed 22,748 women in the Boston area between October 1984 and June 1987.
They were questioned on what they ate and what vitamin supplements they took.
Ten thousand international units of vitamin A is four times the recommended daily
amount. The study showed that 1/57 babies born to women taking vitamin A doses of
greater than 10,000 international units were born with a birth defect.
Jane Brody reports that dosage consumed is proportional to the risk of developing
defects. Higher doses resulted in higher risks. Babies born to women who consumed
more than 10,000 international units daily were 2.4 times as likely to be born with
defects than women who were exposed to only 5,000 international units or less.
The researchers have urged women to not exceed 4,000 to 8,000 international units
daily.
Send comments and suggestions for articles to jlsnell@dartmouth.edu
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
CHANCE News 4.14
(1 October 1995 to 20 October 1995)
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
