!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
CHANCE News 4.10
(2 July 1995 to 20 July 1995)
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Prepared by J. Laurie Snell, with help from William Peterson, Fuxing Hou, Jeanne Albert
and Ma.Katrina Munoz Dy, as part of the CHANCE Course Project supported by the National
Science Foundation. Please send comments and suggestions for articles
to jlsnell@dartmouth.edu
Back issues of Chance News and other materials for teaching a
CHANCE course are available from the Chance Web Data Base.
http://www.geom.umn.edu/locate/chance
==================================================
It is time to tighten up standards of evidence
in historical linquistics. If we enforce rigor,
the truth will enforce itself.
Donald A. Ringe Jr.
==================================================
NOTE: If you would like to join a discussion group to share experiences using current
chance events in class please send a note to jlsnell@dartmouth.edu.
Contents
FROM OUR READERS:
Ruma Falk sent the following comments:
I was interested in your discussion concerning lifetime odds for developing breast
cancer as a function of the woman's age (CHANCE News 4.08) and in Feuer et al.'s
analysis that you presented. For me, this problem triggers a chain of associations.
Here is a ROUGHLY analogous but much simpler problem:
Suppose you are looking for a letter from some time ago. You assess the probability
that the letter is in one of eight (equally likely) drawers of your desk as 0.80.
You start a systematic search of your desk, drawer by drawer. The letter is NOT found
in the first, second,...,ith drawer. After each successive failure to find the letter,
what are the probabilities that the letter will be found in (a) the next drawer (short
range), and (b) some drawer of the desk (long range)?
It is easy to figure out that (a) the short-term probabilities INCREASE as a function
of the number of failures (i), while at the same time the long-term probabilities
DECREASE. The same is true for situations such as waiting for a bus (that you are
not sure is still running) during successive time slots. Some real demographic data show
this to be true also for the probability of getting married within a year versus
ever getting married, as functions of age, in the age range of about 18-30. The discussion
problem you posed -- concerning the increasing (with age) odds that a woman, free of
breast cancer, will develop breast cancer within 10 years versus lifetime odds that
are about constant until age 60 and then decrease -- is quite similar.
We have been studying students' subjective probabilities in situations like these.
Analysis of the results plus discussion of some related situations can be found in
Falk, R., Lipson, A., & Konold, C. (1994).
The ups and downs of the hope function in
a fruitless search. In G. Wright & P. Ayton
(Eds.), Subjective probability (pp. 353-377)
Chichster, England: Wiley.
DISCUSSION QUESTION:
Assume you have eight drawers and a missing letter has an equal chance of being in
each drawer and a 20% chance of not being in any of the drawers. Show that after
each successive failure the probability of finding it in the next drawer increases
but the probability of finding it in some drawer decreases.
<<<========<<
>>>>>==========>>
Eunice Goldberg told us about the next article and provided her own enthusiastic account
of the study being reported. This story make national news: For example Tom Brokaw
talked about it on the evening news and the Washington Post used it as the basis
of an editorial.
Girl finds salary gap could begin at home.
Chicago Tribune, 21 July 1995, News p. 1
Louise Kiernan
This article is about a fourth grade Oak Park girl who wanted a raise in her 50 cents
a week allowance. She decided to conduct a survey to see what other children were
getting. She found that boys averaged more money and had to do fewer chores.
I especially like this article because a child used statistics to try to find information
about something of interest to her. It was truly an authentic task!! I especially
liked the analyses she was willing to do. She compared the lowest girl's salary to
the lowest boy's salary-- as well as the highest. She looked at averages. All of these
issues are of genuine interest to children-- and the math is rich-- especially for
a fourth grader. In addition, the social issue of whether there is discrimination
against females even at very young ages was raised.
I am thinking of doing this survey at Baker Demonstration School in Evanston with
a fourth-fifth grade class. I'll bring up the topic and let the children decide on
what issues they wish to raise. They may decide to interview children in other grades--
we'll see-- and the entire class will work on the analyses
We'll probably have them put their data on spread sheets.
<<<========<<
>>>>>==========>>
He's got their number: Scholar uses math to foil financial fraud.
Wall street journal, 10 July, 1995
Lee Berton
Mark Negrini, who teaches accounting at St. Mary's University in Halifax, wrote his
PhD thesis on: "The detection of income evasion through an analysis of digital distributions".
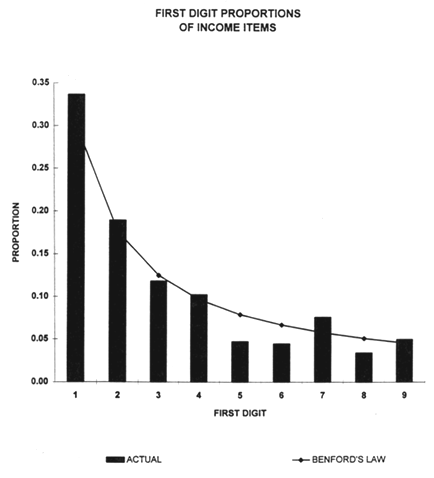
He has persuaded business and government people to use Benford's law to test suspicious financial records such as bookkeeping, checks and tax returns. The article
states that Bendford's law "lays out the statistical frequency with which the numbers
1 through 9 appear in any set of random numbers". Actually, Benford's law states
that the distribution of the leading digit in data sets is typically not equi-distributed
but rather given by the distribution p(k) = log(k+1)- log(k) for k = 1,2,...,9. (The
leading digit of .0034 is 3, of 243 is 2 etc.). Numerous explanations for this have been given but perhaps the most persuasive is that Benford's distribution is the
unique distribution for the leading digits that is not changed by a change of units,
i.e. multiplying the data by a constant c.
(For a recent discussion of Benford's distribution and further references see: Theoredore
P. Hill, The significant digit phenomenon, "The American Mathematical Monthly", April
1995.)
Negrini's idea is that, if we are honest, the numbers in our tax returns and on our
checks should satisfy Benford's law and if they do not there may be some skullduggery.
The article states that "Mr. Negrini has also lent his expertise to federal and state
tax authorities, officials in Denmark and the Netherlands and to several companies.
He has even put President Clinton's tax returns to the Benford's Law test. When
he analyzed the president's returns for the past 13 years he found that 'the returns by
Clinton follow Benford's Law quite closely'".
DISCUSSION QUESTION:
1. Would you expect Benford's distribution to apply to the number of hits a baseball
player gets in a year?, to the prices of stocks on a given day?, to the population
of cities in the United States?
2 Mr. Smith is quite wealthy and makes over a hundred charitable contributions each
year. Do you think the distribution of the leading digits of these numbers would
have a Benford distribution if he is honest? If he cheats, why might they not have
a Benford distribution?
3. Compute the first 100 powers of 2 and show that the leading digits have a Benford
distribution.
<<<========<<
>>>>>==========>>
Time's story on cyberports of questionable validity.
San Francisco Chronicle, 13 July 1995, p C3
Robert Rossney
Martin Rimm, while an undergraduate student of electrical and computer engineering,
did a study of pornography on the Internet which has been recently published in the
Georgetown Law Journal. The July 3, 1995 issue of Time magazine ran a front page
article on the study. The results of the study were widely misinterpreted by congressmen
and others interested in doing something about pornography on the Internet.
A statement in the study that 83.5 percent of all images posted to Usnet are pornography
led Senator Grassley to state in Congress:
The university surveyed 900,000 computer images.
Of these 900,000 images, 83.5 percent of all
computerized photographs available on the
Internet are pornographic. Mr. President, I
want to repeat that: 83.5 percent of the 900,000
images reviewed--these are all on the Internet--
are pornographic, according to the Carnegie Mellon
study.
In the study itself you find that the 83.5% referred to images on the Internet but
only in the binary groups. The percentage was based on a single seven-day period
when the researchers logged 827 image postings to the "non-pornographic" newsgroups
and 4206 image postings to the "pornographic newsgroups." The 900,000 computer files referred
to were not all images and in fact were not on the Internet but rather on adult bulletin
boards.
The study itself and the way it was reported led to a storm of protests on the Internet.
This article reports that Hoffman and Novak, professors who specialize in computer-mediated
marketing, claim that the study's methodology is bad, its definitions are bad, it doesn't study what it purports to study, it's not reproducible, and the authors
disguised the flaws by choosing a publishing venue that would make the study appear
creditable without subjecting it to prepublication peer review.
Well, nothing about the study is disguised now. You can read the study, the original
Time article, and long critiques and replies to the critiques by going to the web
site http://www2000.ogsm.vanderbilt.edu/
DISCUSSION QUESTIONS:
(1) A critic of the study, David Post, writes:
Rimm's conclusion is the precise methodological
equivalent to the following: (a) restricting a
study of printed pornography to magazines located
in the "adult" area of a bookstore, (b) finding
that 83.5% of the reader submissions during a
one-week period were to magazines that contained
"pornographic" material, and concluding (c) that
83.5% of all reader submissions to all magazines
are pornographic.
Do you consider this a fair criticism? Is it a reasonable to compare the availability
of pornography on the Internet with that available in adult bookstores?
(2) Suppose you are given the statistics on the number of people who request any part
of the Chance Database for a one-week period. Could you make a reasonable estimate
for the number of people who read the current issue of Chance News on the Internet?
What would be some of the problems with this estimate?
(3) Do you think Senator Grassley believed what he said?
<<<========<<
>>>>>==========>>
Linguists debating deepest roots of language.
The New York Times, 27 June 1995, Pg. C1
George Johnson
Most linguists do not dispute the hypothesis of a single ancient language that preceded
all Indo-European languages and that was this language family's historical ancestor.
Called Proto-Indo-European (PIE), the words in this language are "reconstructed"
from similar root forms ("cognates") in several languages of the family by using the
rules known to govern how words and even sounds may change over time. For example,
"peace" and "light" in Italian are "pace" and "luce", in Spanish , "paz" and "luz".
Both languages are descendants of the older Latin ("pax" and "lux"). Similarly, Latin
is descendant from PIE, along with Greek and Sanskrit, and many others in the family
are in turn descendant from these.
This article describes recent research on the "Nostratic hypothesis", which claims
that PIE and the languages of five other major groups---Afro-Asiatic, Kartvelian,
Uralic, Dravidian, and Altaic---are all descendant from Nostratic, spoken 12,000
years ago. Unlike enthusiasm for PIE, according to this article linguists are mixed in their
attitudes about Nostratic.
Dr. Donald Ringe, a linguist from the University of Pennsylvania, says that no one
as yet has shown that the similarities between language families are due to anything
but chance variation. Moreover, Ringe deplores his colleagues' lack of "statistical
controls", and in his paper " 'Nostratic' and the Factor of Chance" in the current issue
(Vol. X11, No. 1, 1995) of "Diachronica", he uses a (somewhat vague) application
of the binomial distribution to support his thesis that the six proposed sub-groups
of Nostratic are no more similar than would be expected by chance alone.
DISCUSSION QUESTIONS:
1. Dr. Ringe takes 205 Nostratic roots and for each determines the number of subfamilies
(from 2 to 6) that contain cognate roots (i.e. descendants.) He then determines the
distribution of cognates over these subgroups, and obtains the table:
# of subgroups represented # of roots
2 84
3 70
4 37
5 9
6 5
Thus 84 roots each give rise to a pair of cognates present in exactly two subfamilies,
70 give rise to a triple present in exactly three subfamilies, etc.
Ringe then declares that "this distribution is almost identical with the random distribution
of an event of probability .4 in 6 trials..." What is this random distribution?
What do you think "almost identical" means, and how would you test his claim is
true? Dr. Ringe adds that the .4 distribution "was found by trial and error." What
was his null hypothesis? Is finding such a distribution the same as evidence supporting
the null hypothesis?
2. Suppose you have two lists of 100 words each, each list in a different language,
so that each word is paired with a word that has the same meaning. If you wanted
to see if the two lists are historically related, what would you do?
<<<========<<
>>>>>==========>>
Men at extreme ranges of IQ tests, study says.
Sacramento Bee, 7 July, 1995 A1
Byline: Bee News Services
The article reports that a new study, by Larry Hedges and Amy Nowell of the University
of Chicago, has found that the average man and average woman share about the same
level of intelligence, but men account for a higher proportion of both geniuses and
the mentally deficient. The report analyzed six large national surveys of American male
and female teenagers' performance on tests of mental ability, conducted over the
past thirty years. Their results were presented in "Science" 7 July 1995.
Seven of every eight people in the top 1% of IQ tests are men, but men also represent
an almost equally large percentage of the mentally disadvantaged. Neuroscientist
Richard Haier of the University of California, Irvine, says that the findings of
a higher percent of men in the top IQ levels is nothing new, but what is new is that "there
were more males in the low end."
The article mentions that, while men and women differ in brain sizes and that male
and female brains function differently, such physiological differences do not account
for the differences in the abilities of the sexes. The study sheds little light
on the origin of sex difference in aptitude.
NOTE: In the Science article the authors stress that it is important to analyze representative
samples instead of samples selected from talent searches etc. While they analyze
a number of studies, their main conclusions seem to be based on their analysis of the National Assessment of Educational Progress program which periodically tested
large samples (70,000 to 100,000 students) in the areas of reading, mathematics,
science, and writing. They found that in all four areas the men had higher variances
than the women, typically of the order 3 to 15%. Men had higher average scores in mathematics
and science and the women in reading and writing. They suggest that both the small
number of women in the top 10% of math and science and the high number of men in
the bottom 10% in writing and reading have policy implications. Hedges and Nowell
suggest that intensive recruiting will be necessary to achieve a fair representation
of women in science and that men will have difficulty finding employment in an increasingly information driven economy.
DISCUSSION QUESTIONS:
(1) In their article, the authors state that the difference in the means between men
and women is relatively small while the difference in variances is quite large. They
say that this may help explain the apparent contradiction between the high ratios
of males to females in some highly talented samples and the generally small mean differences
between the sexes in unselected samples. Could this help explain the fact that 60%
of the National Merit Scholarships went to boys this year.
(2) For the sex difference in means, the authors used the standard mean difference--
the difference of the means divided by the standard deviation of the total population.
Why did they not just use the difference in the means?
(3) The article states that men account for a higher proportion of both geniuses and
the mentally deficient. The data in the Science article shows that for verbal skills
there were a higher proportion of women in the top 10% and men in the bottom 10%.
For mathematics skills there were a higher proportion of men in the top 10% and a higher
proportion of women in the bottom 10%. Do you think the article's account describes
this situation reasonably?
<<<========<<
>>>>>==========>>
Senior Class: Reducing the risk for older drivers.
The New York Times, 13 July 1995, C1
Robert W. Stock
Robert Stock describes the different types of tests and research taking place to identify
unsafe older drivers. Fatal accidents involving older drivers and demographics have
forced states and Federal agencies to identify these drivers.
The statistics do not favor older drivers---
A) Measured by the number of miles traveled, older drivers have more crashes, and
more fatal crashes, than most other age groups.
B) Drivers between ages 70 and 74 have 5 fatal crashes for every 100 million miles
of travel---more than double that of drivers 40 to 49.
C) Older drivers drive less but are at more risk when they do.
An accompanying graph is a U-shaped graph giving the proportion of accidents for a
fixed number of miles driven as a function of age. The proportion is largest for
teen-ages smallest for middle-age and then rises for older people becoming to that
equal that of teen-agers.
The author writes that Karlene Ball, a Western Kentucky University researcher, says
that less than 20% of impaired older people have multiple accidents. She says that
researchers should focus on identifying these drivers.
Only 12 states have age-based restrictions on license renewals. States such as California
and New York are considering several driver-control bills. The American Association
of Retired Persons supports legislation that pinpoints impaired drivers based on performance, not age.
The article points out, though, that close to a million older drivers attend refresher
courses each year. It also lists different brochures that can help in the assessment
of an older driver's abilities.
DISCUSSION QUESTION:
The article states that a Yale researcher asked a group of New Haven drivers, ages
72 to 92, questions about their lives and put them through medical tests. A year
later he interviewed them and 13 percent had been involved in an auto accident or
a moving violation. The strongest predictor of trouble turned out to be the drivers' inability
to copy a simple design of two overlapping pentagons. What could copying pentagons
have to do with the ability to drive safely?
<<<========<<
>>>>>==========>>
A new law of physics: stocks will go up, and down.
The Philadelphia Inquirer, 14 July 1995, p A1
Faye Flam
The article is an account of results on the fluctuations of the stock market reported
in the current issues of Nature by physicists Rosario Mantegna and Eugene Stanley,
The wire service account of this was totally mysterious. The account here by Faye
Flam is, I think, an example of first- rate science reporting. To convince you I'll
give Flam's account just as it appears in the article. Here it is:
Stanley and Mantegna read a computer tape that tracked the fluctuations of S&P 500
every 15 seconds for a period of six years, giving them a total of 1.5 million data
points.
To analyze that mass of numbers, they first recorded the size of each tic, then sorted
the ups and downs by size.
Stanley likes to explain it by asking people to imagine making sticks whose lengths
correspond to the size of each dip or rise.
Then imagine taking all the sticks and dumping them on the floor and counting the
number of sticks of each length.
The "distribution" plot they made showed the number of sticks of each length -- which
corresponds to the number of jumps of each size in the market. Most of them were
short, a few were of medium length, and fewer still were long.
If the market fluctuated randomly, they would have seen a "standard distribution."
characterized by a bell-shaped curve.
They saw something different.
"I recognized it right away" Stanley said.
Physicists call it "a Levy walk," a pattern that describes the way particles move
around in turbulent fluids. Corks floating in rough water would follow such a pattern.
The interesting thing about this pattern is that it allows for wild gyrations, such
as the crash of October 1987, Stanley said. This has been considered an aberration,
but according to the turbulent-river model, such things will occur occasionally.
Stanley said that it would be hard to use the model to predict crashes that big--the
market dropped by 22 percent in one day. The model is better for predicting the
frequency of much smaller drops of 3,4, or 5 percent, which can still come as quite
a shock to investors.
This model is bad news for anyone who wants to predict when individual changes will
happen Stanley said.
"No one will ever be able to do that," he said. "If we could do that we'd be very
rich."
DISCUSSION QUESTIONS:
(1) What do you think a sketch of the distribution they found would look like?
(2) How might this information help an investor?
(3) Do you think that if they had chosen an individual stock they would have found
the same distribution?
(4) Why is this bad news for anyone who wants to predict when individual changes
will happen.
<<<========<<
>>>>>==========>>
Data In, Statistics Out -- Maybe.
The Washington Post, 3 July, 1995, F13
William Casey
William Casey presents the problems associated with computer programs designed for
statistical work. Casey contends that today's statistics software packages are powerful
computing tools, but a lack of understanding of the principles behind the software
can lead to inaccurate computations.
He remarks that "No computer program, no matter how good, can substitute for a strong
background of mathematical understanding." Casey sets up the following hypothetical
scenario -- people enter data and produce statistical measures in the form of numbers, tables, and plots. Many software users end up in a formulaic "point and hope" process
--- people eye a collection of specific numbers whose locations on various displays
and printouts they've more or less memorized, and then they draw what they hope are appropriate conclusions.
According to Casey this practice is what leads to inaccurate statistics. Answers
are easy to acquire and "correctness" of the computed statistics is easy to assume.
But in fact, those answers can be wrong. People don't realize their mistakes because
they don't understand what's going on inside the machine.
DISCUSSION QUESTION:
(1) Do you think Casey has a right to be worried?
(2) What do you think Casey means by the "point and hope"
process?
(3) Casey seems to think that the teaching of statistics in the elementary schools
might, in the future, alleviate his concerns. Do you think students who have taken
statistics in college will use their favorite statistical package intelligently when
they analyze data in their work?
<<<========<<
>>>>>==========>>
Ask Marilyn.
Parade Magazine, July 1995, p. 15
Marilyn vos Savant
In her February 26, 1995, column, a reader poses the
following question:
"I'm flying over the China Sea in a single-engine
plane. The same route is being flown by my buddy
in a twin-engine plane. The engines are made by
different companies, but they're the same in all
other respects, such as age, condition and inherent
reliability. It is known that the twin-engine
plane cannot maintain flight on a single engine.
Our destination is hours away. Which plane has a
higher probability of going down because of engine
failure?"
Marilyn says the single engine plane is safer, claiming that if all other factors
are equal, the twin-engine plane is twice as likely to go down.
In a later column, a reader pointed out that her answer could lead to a probability
bigger than one. Marilyn defended her answer, saying the probability is small that
an engine would fail.
Now she reports a letter, from the Deputy Director of the Center for Defense Information,
complaining that her answer is misleading since no manufacturer is permitted to sell
a two-engine aircraft that requires both engines for flight. He is worried that her column will convey too pessimistic a picture of aviation safety.
Marilyn responds that she had to answer the original question in which the twin-engine
plane is known to require both engines to maintain flight. She said that such "if-then"
problems appear in her column because they are good mental exercises and they are entertaining.
DISCUSSION QUESTIONS:
(1) Do you think the Deputy Director's concern is justified?
(2) What do you think of Marilyn's response?
<<<========<<
>>>>>==========>>
New clue to heart disease: A vitamin lack.
The New York Times, 4 July 1995, p 11
Gina Kolata
In the 1960s, Dr. Kilmer McCully hypothesized that people with diets deficient in
folic acid, a B vitamin, are more likely to suffer from heart disease. After being
ignored for thirty years, the 61-year-old pathologist's hypothesis is gaining credence.
Folic acid reduces the amounts in the blood of homocysteine, an amino acid. High levels
of homocysteine can injure blood vessels, causing atherosclerosis and leading to
heart attacks and strokes. Folic acid can reduce heart disease by lowering blood
levels of homocysteine to a safe range.
In 1969, Dr. McCully proposed that large numbers of the population have high homocysteine
levels in their blood, either because of diet or because of genetics. These people
were likely to be at high risk for heart disease and strokes.
Even though a large clinical trial, to see if those with lower homocysteine levels
are more protected from heart disease, is still to be performed, many researchers
have obtained results that support Dr. McCully's hypothesis.
1) Dr. Meier Stampfer, an epidemiology and nutrition professor at Harvard Medical
School, followed 15,000 doctors and found that those who suffered heart attacks had
higher homocysteine levels.
2) Dr. Irwin Rosenberg from Tufts University found a link between clogged carotid
arteries and high homocysteine levels. In his analysis of 1,041 residents of Framingham,
Massachusetts over the age of 67, Dr. Rosenberg found that the higher the homocysteine level, the greater the likelihood of a blocked carotid artery.
Gina Kolata writes that homocysteine levels taper off with the consumption of abundant
amounts of folic acid. This B vitamin is present in dark green leafy vegetables
and orange juice.
DISCUSSION QUESTION:
Why do you think it is so difficult to determine if taking vitamins supplements is
really a good idea?
<<<========<<
>>>>>==========>>
Ask Marilyn.
Parade Magazine, 16 July, 1995 p. 7
Marilyn vos Savant
Marilyn is asked a question that she interprets as follows:
Three people whom we call A, B, and C are allowed to shoot at each other. Shooting attempts rotate cyclically ABCABCABC.... where A has 1/3 chance of hitting his target, B has 1/2 and C has 1. A hit means a kill and the person hit drops out. A participant is also allowed to deliberately miss. What is the chance that each will survive under a rational strategy?
Marilyn's solution is more or less correct but does not lead to the probability of
winning for each player, so Bill Peterson gave us the following more complete solution
to the problem.
First we have to make a convention that prevents them all from choosing the strategy
of firing into the air forever and thus all surving. Presumably we have allowed A
and B to miss deliberately because we could not tell easily if they were doing this.
However, we can tell when C deliberately misses so let's not let him do this. Thus he
must shoot and will hit whomever he shoots at. If A and B are both alive at
the time, C will clearly choose to kill B, and hope that the weaker A will miss the
next shot. It is also clear that neither A nor B would ever want to shoot at the other while
C is still alive, since, if this shot were successful, C would kill the survivor
with the next shot. The surprise is that, on the first shot of the duel A is better
off missing intentionally and letting B try to kill C.
We need two auxiliary calculations to see how A would fare in a two-person shootout
with B if C is somehow eliminated. If A gets the first shot at B, his chance p
satisfies p = 1/3 + (2/3)(1/2)p, since he needs either to hit with his first try
or have B also miss, and the process starts over. This gives p = 1/2. If B gets the first
shot, A's chances are q = (1/2)p = 1/4, since he needs B to miss the first shot,
which again restarts the first process.
Assume now that A starts the duel with a deliberate miss. Knowing that he will next
be shot by C if C is still alive, B will shoot at C. With probability 1/2, C is
killed, and B has a (1-p) = 1/2 chance of surviving the ensuing shootout with A.
Otherwise, C then shoots B, and C has a 2/3 chance of prevailing in the shootout with A.
Thus:
P(C survives) = (1/2)(2/3) = 1/3
P(B survives) = (1/2)(1/2) = 1/4
P(A survives) = 1 - 1/3 - 1/4 = 5/12
To show that this is the optinal choice for all three we need only show that A's initial
decision to miss intentially is optimal for him. We have already said he should
not shoot at B so we have only to show that he should not shoot at C. If A shoots
at C his conditional probability of survival given a miss is exactly the 5/12 just calculated.
On the other hand, a successful shot at C leads to an A-B shootout with B shooting
first, so his conditional probability of survival is q = 1/4 < 5/12. Thus his unconditional probability of survival is less than 5/12 so he is better off intentionally
missing the first shot.
We see that this is an example of survival of the unfittest. A more familiar version
of this problem is the tank problem. Tank A hits with probability 1/6, B with probability
1/3 and C with probability 1/2. In each round, the tanks fire simultaneously and each tank fires at the strongest surviving tank. Then the weakest tank, tank A,
has the best chance of surviving.
<<<========<<
>>>>>==========>>
Some social groups, sports seen slowing academic progress.
The Boston Globe, 11 July 1995, p4
Alice Dembner
This article describes a five-year study conducted by the National Center for Post
Secondary Teaching, Learning and Assessment. The study, involving 4000 undergraduates,
found that playing intercollegiate sports or joining fraternities/sororities slows
the academic progress of college freshmen.
Progress was assessed using standardized tests of reading comprehension, math and
critical thinking. These were administered before the students entered college and
again at the end of their first year. Male football and basketball players scored
lower at the end of the year than when they entered. Even though male athletes outside these
two major sports showed some gains in the course of the year, male athletes as a
whole scored significantly lower than non-athletes in math and reading. Female athletes
showed less improvement than non-athletes in reading comprehension.
In all comparisons, researchers said they controlled for differences in students'
abilities, motivation, number of courses taken, race, socioeconomic status, and other
factors. To explain the results, they suggested an athletic subculture that downplays
academics, and the tendency of athletes to take applied or professional courses rather
than academic ones. A spokesman for the NCAA said the study was of "great concern"
to its members and would figure in future discussions of freshman eligibility.
In similar findings, students in fraternities and sororities scored an average of
8 percentile points lower on all tests than other students. Explanations suggested
were again a non-academic social culture in the groups, and the time demands of rushing
and pledging.
Another part of the study found that minority students and women with off-campus jobs
were 36% more likely to drop out, and those with family obligations were 87% more
likely to drop out.
Finally, a smaller part of the study compared the progress of students with similar
academic talents at two-year and four-year colleges. Interestingly, no significant
differences were found in their progress
<<<========<<
>>>>>==========>>
Cholesterol and life: matter of geography?
The Boston Globe, 13 July 1995, p3
Richard A. Knox
The Seven Countries Study project involving 12,500 men in the U.S., Europe and Japan,
has been an important source of evidence indicating that lowering blood cholesterol
reduces cardiac mortality. A 25-year update of that study verifies that higher cholesterol levels are associated with higher risk of death from heart disease, but it also
finds that the same cholesterol level has different risk levels in different countries.
For example, a middle-aged man with 210 milligrams of cholesterol per deciliter
of blood (this is below the US average) has a 4-5% risk of dying of heart disease within
25 years in Japan, compared with a 12% risk in the US and a 15% risk in Finland.
This suggests that lowering cholesterol alone may not be enough to achieve the low
heart disease risks found in Mediterranean countries like Italy and Greece.
DISCUSSION QUESTIONS:
1. If your cholesterol level is high, should you consider emigrating to Japan? What
other factors might be involved here?
2. Suggest a better title for the article.
<<<========<<
>>>>>==========>>
Ask Marilyn.
Parade Magazine, 18 July 1995, p16
Marilyn vos Savant
A letter from "Herb" in Hayward California asks:
"I live on an earthquake fault, and scientists say a substantial earthquake is going
to occur one of these days. I would rather not move--I have lived here for 20 years--but
I have this unrelenting feeling of doom that, if I stay in the area, I won't live to cash in on my IRA 30 years from now. Is taking a transfer and moving elsewhere
an intelligent thing to do? Moving will cost me serious money! Or are my fears
making me do something irrational? What does 'probability' say about escaping from
a pending earthquake disaster?"
Marilyn says that, if an earthquake struck, Herb's chances of surviving would be high.
She notes that, in the recent Kobe quake in Japan, 97.865% of the population suffered
no bodily harm, while only .347% were killed and 1.788% were injured. However, she adds that moving would reduce his chances of experiencing an earthquake. She diplomatically
concludes that staying or moving could each be rational conclusions.
DISCUSSION QUESTIONS:
1. To what population do you think Marilyn's percentages refer?
2. In what sense do they represent a reasonable answer to Herb's question about his
probability of escape from an earthquake disaster?
<<<========<<
>>>>>==========>>
Pro and con: guns and neuroses.
The San Francisco Examiner, 17 July 1995, p A13.
Bonnie Erbe and Betsy Hart
This month Virginia became the 25th state to allow citizens to carry concealed weapons.
Advocates of such measures maintain that they will reduce crime. Gun control groups
have long insisted that legally owned handguns are much more likely to be involved in fatal accidents, suicides and homicides among people who know each other than
they are in preventing crimes. The two authors of this article argue over the statistics
cited by each camp.
Erbe states that the only impartial (as opposed to NRA-backed) study in recent years
was a University of Maryland study this spring, in which researchers investigated
five cities (Miami, Jacksonville, Tampa, Portland and Jackson, Mississippi) in states
where concealed weapons laws had been enacted. In four of these cities, firearm related
homicides jumped (by as much as 74%) after the laws.
Hart replies that this study was flawed and claims that the researchers skewed the
results by calculating crime rates from the early 1970s. She says that in Miami,
Jacksonville and Tampa, homicide rates declined 10%, 18% and 20% respectively after
Florida enacted the law. She cites Justice Dept. figures that 645,000 Americans each year
used handguns for protection against criminals, and an additional 300,000 protective
uses occur with rifles and shotguns. Finally, she notes that a Justice Dept. survey
of felons found that 80% of those using handguns had encountered armed citizens, and
53% did not commit at least one crime for fear that the victim was armed.
DISCUSSION QUESTIONS:
1. Do you think that Florida's law actually prevents homicides? Do you think this
is what the measure is designed to do? (see also next article).
2. How do you think the number of protective uses of handguns was estimated? What
difficulties do you foresee? Is 645,000 is a "large number" of averted crimes?
3. Do you think felons are inclined to respond honestly to surveys on their criminal
activities?
<<<========<<
>>>>>==========>>
The great gun debate: get the picture?
US News and World Report, 17 July 1995, p7
Ted Gest
The "picture" accompanying the article shows a mild-mannered- looking Virginia woman
being photographed for her permit to carry a concealed weapon. Relevant to the discussion
above, the article notes that "when Florida liberalized its concealed weapons law in 1987, advocates predicted a decline in crime and critics warned of a blood bath
when would-be victims shot it out with would-be assailants. Both were wrong. Homicides
actually dropped--but violent crime increased overall."
<<<========<<
>>>>>==========>>
Ask Mr. Statistics.
Fortune, 24 July, 1995, pp. 170-171
Daniel Seligman
Mr. Statistics is asked how he feels about the recent claim of a breakthrough announced
by Marvin Runyon on June 13 under the headline SERVICE BREAKS ALL RECORDS ANNOUNCED
POSTMASTER GENERAL. The record broken was overnight delivery of first-class mail
at an 87% rate nationwide. Apparently, Mr. Statistics has been critical of the post
office in the past.
Mr. Statistics replies by saying that he has carried out his own experiment to test
this claim. He mailed a letter to himself on each of the ten days between the press
release and the deadline for this article, recording the date and time the letter
was sent. He mailed each letter at a letterbox within a block of his own residential tower
and within three blocks of the Lenox Hill Post Office. All the pickups should have
taken place no later than 3 P.M. and should have been treated as next-day delivery
missives. Only four of these ten letters were delivered overnight.
Mr. Statistics remarks that the post office only claimed 83% for New York City. He
showed his reader how to find the probability that, with a 83% probability for success,
you would get 4 or less successes. He finds this probability to be .27% and so is
inclined to not believe the press release.
DISCUSSION QUESTIONS:
(1) How do you think a test like this would turn out in your area?
(2) Does this experiment suggest the claim for New York City as a whole is not correct
or just for the area where Mr. Statistics lives?
<<<========<<
>>>>>==========>>
Cancer link contradicted by new Harman study.
The New York Times, 12 July 1995, A1
Gina Kolata
Just a month after a study showed hormone replacement therapy after menopause increases
the risk of breast cancer, a new study does not find any increased risk.
This study, just published in the "Journal of the American Medical Association", compared
some 500 women aged 50 to 64, newly diagnosed to have breast cancer, with a similar
group of healthy women. Researchers found that women who had used harmones for eight years or longer had, if anything, a lower risk of breast cancer.
The earlier study, published in the June 15, 1995 issue of the "New England Journal
of Medicine" followed 122,000 nurses for 14 years and found that hormone replacement
increased the risk of breast cancer by 30 to 70 percent.
The article gives a number of expert's reactions to the studies and discusses the
general question of advising women on the pros and cons of prescribing hormone treatments.
DISCUSSION QUESTIONS:
(1) What are the differences in design of these two studies?
How might these differences contribute to different outcomes?
(2) The author of the present study said the nurses' study may have been biased because
women taking hormone replacement therapy "are more likely to be in contact with the
health care community and more likely to be receiving mammograms and breast exams,"
with the resulting greater likelihood of a breast cancer diagnosis.
The author of the previous study said that the newer study might have missed an effect
because it was smaller and because as many as 30 percent of the women who were prospective
subjects had declined to be interviewed.
What do you conclude from these remarks?
<<<========<<
>>>>>==========>>
We have some additional comments on the following two articles mentioned in the last
Chance News:
Propensity to Abuse---Propensity to Murder?
Chance Magazine, Spring 1995, p 14.
Jon F. Merz and Jonathan P. Caulkins
and
When batterer turns murderer.
Nature, 15 June 1995, p. 541
I. J. Good.
Recall that Alan Dershowitz, on the O. J. Simpson defense team, stated on T.V. and
in newspapers that only one-tenth of one percent of men who abuse their wives go
on to murder them. He clearly wanted his audience to interpret this to mean that
the evidence of abuse by Simpson would only suggest a 1 in 1,000 chance of his being guilty
of murdering her.
Both authors believe the jury would be more interested in the probability that the
husband is guilty of the murder of his wife given that he abused his wife and his
wife was murdered. They both solve this problem by using Bayes' theorem, but their
solutions differ in an interesting way.
Let A be the event that a man has abused his wife, M that the wife is murdered, and
G that the man is guilty of murdering his wife.
We need to find P[G|A,M]. Jeanne Albert pointed out that we can write this as P[G|A,M]
= P[G|A]/P[M|A]. From this we see that the desired probability is at least 1/2 if
at least 1/2 of the abused women who are murdered are murdered by their spouses.
It seems reasonable that this is true but we would have to look at the data.
Merz and Caulkins write the desired odds ratio as
P(G|A,M)/P(~G|A,M) = P(G|M)/P(~G|M) * P(A|G,M)/P(A|~G,M)
and Good writes it as
P(G|A,M)/P(~G|A,M) = P(G|A)/P(~G|A) * P(M|G,A)/P(M|~G,A).
Consequently, they need different kinds of information to answer the question.
Merz and Caulkins say that, of the 4936 women who were murdered in 1992, about 1430
were killed by their husband or boyfriend, giving an estimate of .29 for P(G|M).
In a newspaper article, Dershowitz stated that "It is, of course, true that, among
the small number of men who do kill their present or former mates, a considerable number
did first assault them." Merz and Caulkins interpret "a considerable number" to be
1/2. This gives them P(A|G,M) = .5. Finally, they assume that the probability of
a wife's being abused by her husband, given that she was murdered by someone else, is the
same as the probability of a randomly chosen wife's being
abused. They say that this has been estimated to be .05. This gives an odds ratio
of 4.08, with corresponding probability .81 of a husband's being guilty, given that
he has abused his wife and she has been murdered.
Good needs first to estimate P(G|A). He starts with Dershowitz's estimate of 1/1000
that the abuser will murder his wife. He assumes the probability is at least 1/10
that this will happen in the year in question. Thus P(G|A) is at least 1/10,000.
Of course P(M|G,A) = 1, so he is left only with estimating P(M|~G,A). For this he says
that there are about 25,000 murders a year in the U.S. population of 250,000,000.
Thus he estimates P(M|~G,A) to be 1/10,000. This gives him an odds ratio of 1 with
corresponding probability .5 for the husband being guilty, given that he had abused his wife
and she was murdered.
Since they have had to make some rather arbitrary assumptions to get their estimates,
it is not surprising that they get quite different answers. However, the true probability
is surely much larger than the .001 probability that Dershowitz obviously hoped the jury in the O. J. Simpson case would think was the appropriate probability.
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
CHANCE News 4.10
(2 July 1995 to 20 July 1995)
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
